题目内容
1.40=1${({-\frac{1}{2}})^{-2}}$=4
(2a-1b)3=$\frac{8{b}^{3}}{{a}^{3}}$.
分析 根据零指数幂和负整数指数幂的运算法则计算即可.
解答 解:40=1; ${({-\frac{1}{2}})^{-2}}$=$\frac{1}{(-\frac{1}{2})^{2}}$=$\frac{1}{\frac{1}{4}}$=4;(2a-1b)3=8a-3b3=$\frac{8{b}^{3}}{{a}^{3}}$.
故答案为:1;4;$\frac{8{b}^{3}}{{a}^{3}}$.
点评 本题主要考查的是负整数指数幂和零指数幂的运算,掌握负整数指数幂和零指数幂的运算法则是解题的关键.

练习册系列答案
相关题目
12. 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于4,则△ABC的面积等于( )| A. | 12 | B. | 16 | C. | 24 | D. | 36 |
9.计算$\sqrt{16}$的平方根结果是( )
| A. | ±2 | B. | ±4 | C. | 2 | D. | 4 |
6. 已知二次函数的解析式是y=x2-2x-3.
已知二次函数的解析式是y=x2-2x-3.
(1)与x轴的交点坐标是(-1,0),(3,0),顶点坐标是(1,-4);
(2)在坐标系中利用描点法画出此抛物线;
(3)结合图象回答:当-2<x<2时,函数值y的取值范围是当-2<x<1时,-4<y<5;当1<x<2时,-4<y<-3.
 已知二次函数的解析式是y=x2-2x-3.
已知二次函数的解析式是y=x2-2x-3.(1)与x轴的交点坐标是(-1,0),(3,0),顶点坐标是(1,-4);
(2)在坐标系中利用描点法画出此抛物线;
| x | … | … | |||||
| y | … | … |
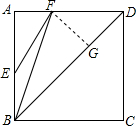 已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.
已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD. 如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,第2016次输出的结果为6.
如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9,第2016次输出的结果为6. 小聪用一条长21米的绳子,借助一面墙围,成了如图所示的长方形.
小聪用一条长21米的绳子,借助一面墙围,成了如图所示的长方形.