��Ŀ����
18��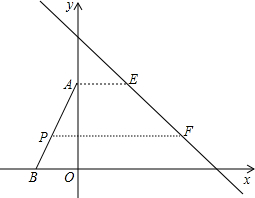 ��ͼ����ABO�Ķ���A��B������ֱ�Ϊ��0��4������-2��0����ֱ��l��x����C����y����D����������Ӧ�ĺ�������ʽΪy=-x+6���涨������ƽ���ϵ�ijһ��M��������ˮƽ���ҵķ���ƽ�ƣ�ƽ�Ƶ�ֱ��l��Ϊֹ�����������ƽ�Ƶľ��룬��Ϊ��M�ġ���ƽ�ƾ��롱��
��ͼ����ABO�Ķ���A��B������ֱ�Ϊ��0��4������-2��0����ֱ��l��x����C����y����D����������Ӧ�ĺ�������ʽΪy=-x+6���涨������ƽ���ϵ�ijһ��M��������ˮƽ���ҵķ���ƽ�ƣ�ƽ�Ƶ�ֱ��l��Ϊֹ�����������ƽ�Ƶľ��룬��Ϊ��M�ġ���ƽ�ƾ��롱����1������ֱ��д��D�����ꡢA��ġ���ƽ�ƾ��롱��AE�ij��ȣ���ֱ��AB�ı���ʽ��
��2�����߶�AB����һ��P�ġ���ƽ�ƾ��롱PF=6�������P������ꣻ
��3����ij��ġ���ƽ�ƾ��롱������6����Ƹõ�Ϊ����ȫ�㡱���ڡ�ABO���ڲ�����ϵ����С���ȫ�㡱������һ��������������������������
���� ��1�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�D��E������꣬����ƽ����x���ֱ���������ľ����ǽϴ�ĺ��������С�ĺ����꣬�ɵ�AE�ij����ٸ��ݴ���ϵ�������ɵ�AB�Ľ���ʽ��
��2�����ݵ���ֱ���ϣ��ɵ�P��F������꣬����PF�ľ��룬�ɵù���b�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��3������ƽ�����ƽ���߶���ȣ��ɵ�PO�ϵĵ��ǰ�ȫ�㣬�߶�AP�ϵĵ��ǰ�ȫ�㣬�ٸ��������ε������ʽ���ɵô𰸣�
��� �⣺��1����x=0ʱ��y=6����D��0��6����
��y=4ʱ��-x+6=4�����x=2����E��2��4����
AE�ij�Ϊ2-0=2��
��AB�Ľ���ʽΪy=kx+b����A��0��4����B��-2��0�����뺯������ʽ����
$\left\{\begin{array}{l}{-2k+b=0}\\{b=4}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$��
ֱ��AB�ı���ʽy=2x+4��
��2�����߶�AB����һ��P����P��$\frac{b-4}{2}$��b����
��F��CD�ϣ���F��6-b��b����
��PF�ij�Ϊ6����
6-b-$\frac{b-4}{2}$=6��
���b=$\frac{4}{3}$��
$\frac{b-4}{2}$=$\frac{\frac{4}{3}-4}{2}$=-$\frac{4}{3}$��
��P��-$\frac{4}{3}$��$\frac{4}{3}$����
��3����ͼ��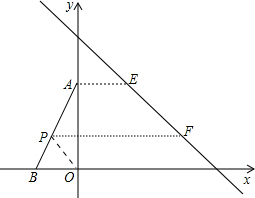
��P��ƽ��CD�Ľ���ʽΪy=-x��
PO�ϵĵ��ǰ�ȫ�㣬AP�ϵĵ��ǰ�ȫ�㣬
��APO�ǰ�ȫ����
S��APO=$\frac{1}{2}$AO•|Px|=$\frac{1}{2}$��4��|-$\frac{4}{3}$|=$\frac{8}{3}$��
���� ���⿼����һ�κ����ۺ��⣬�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ�������꣬��2������ƽ����x���ֱ���������ľ����ǽϴ�ĺ��������С�ĺ�����ó�����b�ķ����ǽ���ؼ�����3��������ƽ�����ƽ���߶���ȳ���PO�ϵĵ��ǰ�ȫ���ǽ���ؼ���

 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�| A�� | ��2 | B�� | ��4 | C�� | 2 | D�� | 4 |
 ��֪���κ����Ľ���ʽ��y=x2-2x-3��
��֪���κ����Ľ���ʽ��y=x2-2x-3����1����x��Ľ��������ǣ�-1��0������3��0�������������ǣ�1��-4����
��2��������ϵ��������㷨�����������ߣ�
| x | �� | �� | |||||
| y | �� | �� |
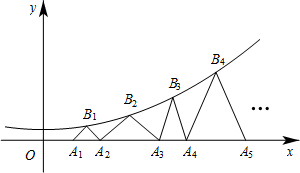 ��ͼ����֪������y=a1x2+c������B1��1��$\frac{1}{3}$����B2��2��$\frac{7}{12}$�����ڸ���������ȡ��B3��3��y3����B4��4��y4����Bn��n��yn����x��������ȡ��A1��A2������An��ʹ��A1B1A2����A2B2A3���ֱ����ԡ�B1����B2��������BnΪ���ǵĵ��������Σ���A1�ĺ�����Ϊt��0��t��1������
��ͼ����֪������y=a1x2+c������B1��1��$\frac{1}{3}$����B2��2��$\frac{7}{12}$�����ڸ���������ȡ��B3��3��y3����B4��4��y4����Bn��n��yn����x��������ȡ��A1��A2������An��ʹ��A1B1A2����A2B2A3���ֱ����ԡ�B1����B2��������BnΪ���ǵĵ��������Σ���A1�ĺ�����Ϊt��0��t��1������