题目内容
14. 如图,在等边△ABC中,点E、F分别在AB、BC边上,且AE=BF=$\frac{1}{3}$AB,连接AF、CE交于点G,将△ABC沿AC翻折得到△ACD,连接DG,且DG=6$\sqrt{7}$,过点D作∠CDG的角平分线交CB于M,则四边形DGFM的面积是77$\sqrt{3}$-$\frac{49\sqrt{21}}{3}$.
如图,在等边△ABC中,点E、F分别在AB、BC边上,且AE=BF=$\frac{1}{3}$AB,连接AF、CE交于点G,将△ABC沿AC翻折得到△ACD,连接DG,且DG=6$\sqrt{7}$,过点D作∠CDG的角平分线交CB于M,则四边形DGFM的面积是77$\sqrt{3}$-$\frac{49\sqrt{21}}{3}$.
分析 先证△ACE≌△ABF得∠ACE=∠BAF,由∠CGF=∠CAG+∠ACE=∠CAG+∠BAF=∠BAC=∠ADC=60°知点A、D、C、G四点共圆,得∠AGD=∠ACD=60°,∠DGC=∠DAC=60°,作FK⊥AB于点K,设BK=t,则AE=BF=$\frac{BK}{cosB}$=2t,FK=$\sqrt{3}$t,AB=3BF=6t、AK=5t、AF=2$\sqrt{7}$t,证△AGE∽△ABF得AG=$\frac{6\sqrt{7}}{7}$t,作AP⊥DG,得PG=AGcos∠AGD=$\frac{3\sqrt{7}}{7}$t、AP=AGsin∠AGD=$\frac{3\sqrt{21}}{7}$t、PD=$\sqrt{A{D}^{2}-A{P}^{2}}$=$\frac{15\sqrt{7}}{7}$t,由DG=PD+PG可得t=$\frac{7}{3}$,即可知AD=14,AF=$\frac{14\sqrt{7}}{3}$,AP=$\sqrt{21}$,延长DM、AF交于点N,证BC∥AD、FM=FN得AD=AN=14、FM=FN=AN-AF=14-$\frac{14\sqrt{7}}{3}$,作BQ⊥DA交DA延长线于点Q,则BQ=ABsin∠BAQ=7$\sqrt{3}$,最后根据S四边形DGFM=S梯形ADMF-S△ADG可得答案.
解答 解:如图,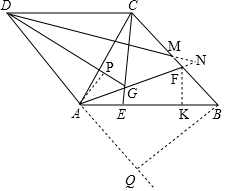
∵△ABC是等边三角形,
∴AC=AB,∠CAE=∠BAF=60°,
在△ACE和△ABF中,
∵$\left\{\begin{array}{l}{AC=AB}\\{∠CAE=∠BAF}\\{AE=BF}\end{array}\right.$,
∴△ACE≌△ABF,
∴∠ACE=∠BAF,
∴∠CGF=∠CAG+∠ACE=∠CAG+∠BAF=∠BAC=∠ADC=60°,
∴点A、D、C、G四点共圆,
∴∠AGD=∠ACD=60°,∠DGC=∠DAC=60°,
作FK⊥AB于点K,
设BK=t,则AE=BF=$\frac{BK}{cosB}$=$\frac{t}{cos6{0}^{°}}$=2t,FK=$\sqrt{B{F}^{2}-B{K}^{2}}$=$\sqrt{3}$t,
∴AB=3BF=6t,AK=AB-BK=5t,AF=$\sqrt{A{K}^{2}+F{K}^{2}}$=2$\sqrt{7}$t,
∵△ACE≌△ABF,
∴∠AEG=∠AFB,
∵∠GAE=∠BAF,
∴△AGE∽△ABF,
∴$\frac{AG}{AB}=\frac{AE}{AF}$,即$\frac{AG}{6t}=\frac{2t}{2\sqrt{7}t}$,
则AG=$\frac{6\sqrt{7}}{7}$t,
作AP⊥DG于点P,
∴PG=AGcos∠AGD=$\frac{6\sqrt{7}}{7}t$•$\frac{1}{2}$=$\frac{3\sqrt{7}}{7}$t,AP=AGsin∠AGD=$\frac{6\sqrt{7}}{7}t$•$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{21}}{7}$t,
则PD=$\sqrt{A{D}^{2}-A{P}^{2}}$=$\frac{15\sqrt{7}}{7}$t,
由DG=PD+PG可得$\frac{15\sqrt{7}}{7}$t+$\frac{3\sqrt{7}}{7}$t=6$\sqrt{7}$,
解得t=$\frac{7}{3}$,
则AD=6t=14,AF=2$\sqrt{7}$t=$\frac{14\sqrt{7}}{3}$,AP=$\frac{3\sqrt{21}}{7}$t=$\sqrt{21}$,
延长DM、AF交于点N,
∵∠GDN=∠CDM、∠DCM=∠DGN=120°,
∴∠FMN=∠DMC=∠N,
∴FM=FN,
又∵∠ACB=∠CAD=60°,
∴BC∥AD,
∴∠FMN=∠ADN=∠N,
∴AD=AN=14,
∴FM=FN=AN-AF=14-$\frac{14\sqrt{7}}{3}$,
作BQ⊥DA交DA延长线于点Q,
则BQ=ABsin∠BAQ=14×$\frac{\sqrt{3}}{2}$=7$\sqrt{3}$,
∴S四边形DGFM=S梯形ADMF-S△ADG
=$\frac{1}{2}$×(14-$\frac{14\sqrt{7}}{3}$+14)×7$\sqrt{3}$-$\frac{1}{2}$×6$\sqrt{7}$×$\sqrt{21}$
=77$\sqrt{3}$-$\frac{49\sqrt{21}}{3}$,
故答案为:77$\sqrt{3}$-$\frac{49\sqrt{21}}{3}$.
点评 本题主要考查翻折变换的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理、四点共圆的条件等知识点的综合运用,熟练掌握、灵活运用这些知识点是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 7 | B. | -7 | C. | 1 | D. | -1 |
 现有某教学网站策划了A、B两种上网学习的月收费方式:
现有某教学网站策划了A、B两种上网学习的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 7 | 25 | 0.01 |
| B | m | n | 0.01 |
(1)如图是yB与x之间函数关系的图象,请根据图象填空:m=10;n=50
(2)写出yA与x之间的函数关系式.
(3)选择哪种方式上网学习合算,为什么?
 已知实数a,b在数轴上的位置如图所示,下列结论正确的是( )
已知实数a,b在数轴上的位置如图所示,下列结论正确的是( )| A. | b<$\frac{1}{a}$<-b<a | B. | b<-b<$\frac{1}{a}$<a | C. | $\frac{1}{a}$<b<a<-b | D. | -b<$\frac{1}{a}$<a<b |
| A. | 众数是88 | B. | 中位数是88 | C. | 平均数是88 | D. | 方差是88 |
