题目内容
2.已知反比例函数y=$\frac{m}{x}$的图象位于二、四象限内,则关于x的方程(m+1)x2-2x+1=0根的情况是( )| A. | 有一个或两个实数根 | B. | 仅有一个实数根 | ||
| C. | 有两个实数根 | D. | 没有实数根 |
分析 由反比例函数图象在二、四象限内,可得知其系数m<0,再将方程(m+1)x2-2x+1=0中的系数代入b2-4ac中求出△=-4m>0,由此得出结论.
解答 解:∵反比例函数y=$\frac{m}{x}$的图象位于二、四象限内,
∴m<0.
在方程(m+1)x2-2x+1=0中,
△=b2-4ac=(-2)2-4(m+1)=-4m>0,
∴关于x的方程(m+1)x2-2x+1=0有两个不相等的实数根.
故选C.
点评 本题考查了反比例函数的性质以及根的判别式,解题的关键是找出关于x的方程(m+1)x2-2x+1=0的根的判别式的符号.本题属于基础题,难度不大,解决该题型题目时,先根据反比例函数图象所在的象限得出其系数m的取值范围,再根据二次方程的系数找出其根的判别式的正负是关键.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
12.已知方程x2+kx-6=0的一个根是x=2,则它的另一个根为( )
| A. | x=1 | B. | x=-2 | C. | x=3 | D. | x=-3 |
13.2015年6月国家主席习大大和比利时国王菲利普,在人民大会堂共同见证了两国公司在集成电路方面进行合作研发的签约仪式,两国将共同着力研发14纳米量产技术,这标志着我国芯片制造能力将进入国际顶尖水平.14纳米为0.000 000 014米,将0.000 000 014用科学记数法表示应为( )
| A. | 0.14×10-7 | B. | 1.4×10-8 | C. | 0.014×10-6 | D. | 14×10-9 |
17. 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
7.小明掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,那么向上一面的点数大于4的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
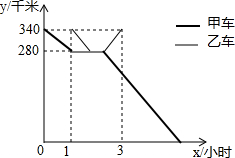 已知重庆和成都相距340千米,甲车早上八点从重庆出发往成都运送物资,行驶1小时后,汽车突然出现故障,立即通知技术人员乘乙车从重庆赶来维修(通知时间不计),乙车达到后经30分钟修好甲车,然后以原速返回重庆,同时甲车以原来速度的1.5倍继续前往成都.两车分别距离成都的路程y(千米)与甲车所用时间x(小时)之间的函数图象如图所示,下列四个结论:①甲车提速后的速度是90千米/时;②乙车的速度是70千米/时;③甲车修好的时间为10点15分;④甲车达到成都的时间为13点15分,其中,正确的结论是①③(填序号)
已知重庆和成都相距340千米,甲车早上八点从重庆出发往成都运送物资,行驶1小时后,汽车突然出现故障,立即通知技术人员乘乙车从重庆赶来维修(通知时间不计),乙车达到后经30分钟修好甲车,然后以原速返回重庆,同时甲车以原来速度的1.5倍继续前往成都.两车分别距离成都的路程y(千米)与甲车所用时间x(小时)之间的函数图象如图所示,下列四个结论:①甲车提速后的速度是90千米/时;②乙车的速度是70千米/时;③甲车修好的时间为10点15分;④甲车达到成都的时间为13点15分,其中,正确的结论是①③(填序号)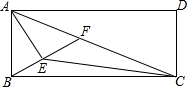 如图,在矩形ABCD中,AB=5,AD=12,AC是它的一条对角线,AE平分∠BAC,BE⊥AE于点E,交AC于点F,连接CE,则四边形AECD的面积是45.
如图,在矩形ABCD中,AB=5,AD=12,AC是它的一条对角线,AE平分∠BAC,BE⊥AE于点E,交AC于点F,连接CE,则四边形AECD的面积是45.