题目内容
19.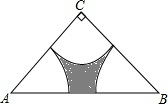 如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以$\frac{1}{2}$AC为半径画弧,求三条弧与边AB所围成的阴影部分的面积.
如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以$\frac{1}{2}$AC为半径画弧,求三条弧与边AB所围成的阴影部分的面积.
分析 由于三条弧所对的圆心角的和为180°,根据扇形的面积公式可计算出三个扇形的面积和,而三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和,再利用三角形的面积公式计算出S△ABC=$\frac{1}{2}$×4×4=8,然后代入即可得到答案.
解答 解:∵∠C=90°,CA=CB=4,
∴$\frac{1}{2}$AC=2,S△ABC=$\frac{1}{2}$×4×4=8,
∵三条弧所对的圆心角的和为180°,
三个扇形的面积和=$\frac{180π×{2}^{2}}{360}$=2π,
∴三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和=8-2π.
点评 本题考查了扇形的面积公式:S=$\frac{nπ{R}^{2}}{360}$以及考查了等腰直角三角形的性质,得出阴影部分的面积=S△ABC-三个扇形的面积和是解题关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.下列说法正确的是( )
| A. | 哥哥的身高比弟弟高是必然事件 | |
| B. | 今年中秋节有雨是不确定事件 | |
| C. | 随机抛一枚均匀的硬币两次,都是正面朝上是不可能事件 | |
| D. | “彩票中奖的概率为$\frac{1}{5}$”表示买5张彩票肯定会中奖 |
14. 如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
(1)S△AOE=S△COE; (2)S△AOB=S四边形EODC;
(3)S△BOC=2S△COE; (4)S△ABC=4S△BOC.
 如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )
如图,AD、BE是△ABC的中线,则下列结论中,正确的个数有( )(1)S△AOE=S△COE; (2)S△AOB=S四边形EODC;
(3)S△BOC=2S△COE; (4)S△ABC=4S△BOC.
| A. | .1个 | B. | .2个 | C. | .3个 | D. | .4个 |
4.顺次连结任意四边形各边中点所得到的四边形一定是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
11.3月15日是国际消费者权益日.某品牌专卖店准备出售甲、乙两种服装.其中甲、乙两种服装的进价和售价如表:
已知:专卖店用3000元购进甲种服装的数量与用2400元购进乙种服装的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种服装共200件的总利润(利润=售价-进价)不少于21700元,且甲种服装的件数不超过总件数的一半,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(50<a<70)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
| 服装价格 | 甲 | 乙 |
| 进价(元/件) | m | m-20 |
| 售价(元/件) | 240 | 160 |
(1)求m的值;
(2)要使购进的甲、乙两种服装共200件的总利润(利润=售价-进价)不少于21700元,且甲种服装的件数不超过总件数的一半,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(50<a<70)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
 如图,在△ABC中,∠C=60°,且高BE经过高AD的中点F.求证:BF=4EF.
如图,在△ABC中,∠C=60°,且高BE经过高AD的中点F.求证:BF=4EF.