题目内容
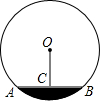 如图,AB是⊙O的弦,OC⊥AB于C,且OC=
如图,AB是⊙O的弦,OC⊥AB于C,且OC=| 1 |
| 2 |
考点:扇形面积的计算,垂径定理
专题:
分析:如图,连接OA、OB.根据垂径定理、勾股定理可以求得OA的长度,然后根据S阴影=S扇形OAB-S△OAB.
解答: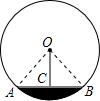 解:如图,连接OA、OB.
解:如图,连接OA、OB.
∵AB是⊙O的弦,OC⊥AB于C,且OC=
AB=2,
∴∠ACO=90°,AC=
AB=2,
∴AC=OC,
∴∠AOC=∠OAC=45°,
∴∠AOB=90°.
在直角△AOC中,由勾股定理得到:OA=
=
=2
.
∴S阴影=S扇形OAB-S△OAB=
-
×4×2=2π-4,即图中阴影部分的面积是(2π-4).
 解:如图,连接OA、OB.
解:如图,连接OA、OB.∵AB是⊙O的弦,OC⊥AB于C,且OC=
| 1 |
| 2 |
∴∠ACO=90°,AC=
| 1 |
| 2 |
∴AC=OC,
∴∠AOC=∠OAC=45°,
∴∠AOB=90°.
在直角△AOC中,由勾股定理得到:OA=
| AC2+OC2 |
| 22+22 |
| 2 |
∴S阴影=S扇形OAB-S△OAB=
| 90π×8 |
| 360 |
| 1 |
| 2 |
点评:本题考查了垂径定理,扇形面积的计算.求阴影部分的面积时,利用了“分割法”.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图所示的图形绕虚线旋转一周,所形成的几何体是( )
如图所示的图形绕虚线旋转一周,所形成的几何体是( )A、 |
B、 |
C、 |
D、 |
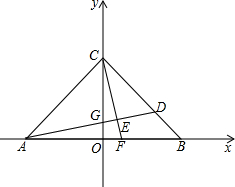 如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的
如图,在平面直角坐标系中,OA=OB=OC=6,过点A的直线AD交BC于点D,交y轴与点G,△ABD的面积为△ABC面积的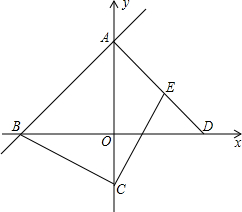 已知,如图:直线AB:y=x+8与x轴、y轴分别相交于点B、A,过点A作直线AB的垂线交x轴于点D.
已知,如图:直线AB:y=x+8与x轴、y轴分别相交于点B、A,过点A作直线AB的垂线交x轴于点D.