题目内容
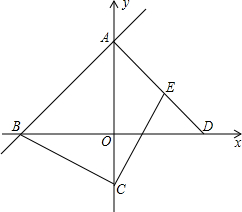 已知,如图:直线AB:y=x+8与x轴、y轴分别相交于点B、A,过点A作直线AB的垂线交x轴于点D.
已知,如图:直线AB:y=x+8与x轴、y轴分别相交于点B、A,过点A作直线AB的垂线交x轴于点D.(1)求证:△AOB≌△AOD;
(2)求A、D两点确定的直线的函数关系式;
(3)若点C是y轴负半轴上的任意一点,过点C作BC的垂线与AD相交于点E,请你判断:线段BC与CE的大小关系?并证明你的判断.
考点:一次函数综合题
专题:
分析:(1)通过ASA证明△AOB≌△AOD;
(2)根据全等三角形的性质可得OD=OB=8,则D(0,8),再根据待定系数法可得直线AD的函数关系式;
(3)过点C作CF⊥y轴,交直线AB于点F,ASA证明△ACE≌△FCB,再根据全等三角形的性质即可求解.
(2)根据全等三角形的性质可得OD=OB=8,则D(0,8),再根据待定系数法可得直线AD的函数关系式;
(3)过点C作CF⊥y轴,交直线AB于点F,ASA证明△ACE≌△FCB,再根据全等三角形的性质即可求解.
解答:(1)解:对于直线y=x+8,
令x=0,求得y=8;令y=0,求得x=-8,
∴A(0,8),B(-8,0),
∴OA=OB=8,
∴∠ABO=∠BAO=45°,
又∵DA⊥AB,
∴∠OAD=90°-∠OAB=45°,
∴∠BAO=∠OAD,
又∵∠AOB=∠DOB=90°,
在△AOB和△AOD中,
,
∴△AOB≌△AOD(ASA),
(2)解:∵△AOB≌△AOD,
∴OD=OB=8,
∴D(8,0),
设AD的解析式为y=kx+b,则
解得k=-1,b=8.
∴AD的解析式为y=-x+8.
(3)BC=CE,
证明:过点C作CF⊥y轴,交直线AB于点F,
∵BC⊥CE,
∴∠BCE=∠ACF=90°,
∴∠BCF=∠ACE,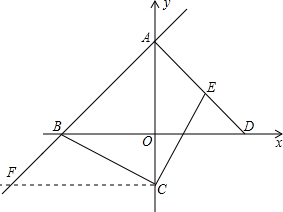
又∵∠OAB=∠OAD=45°,
∴∠CFA=90°-45°=∠OAD,
∴∠BAC=∠AFC,
∴CA=CF,
在△ACE和△FCB中
,
∴△ACE≌△FCB(ASA),
∴BC=CE.
其它方法一:连接CD,然后证CD=CE;方法二:过点C作CG⊥y轴,交直线AD于点G,证△ECG≌△BCA.
令x=0,求得y=8;令y=0,求得x=-8,
∴A(0,8),B(-8,0),
∴OA=OB=8,
∴∠ABO=∠BAO=45°,
又∵DA⊥AB,
∴∠OAD=90°-∠OAB=45°,
∴∠BAO=∠OAD,
又∵∠AOB=∠DOB=90°,
在△AOB和△AOD中,
|
∴△AOB≌△AOD(ASA),
(2)解:∵△AOB≌△AOD,
∴OD=OB=8,
∴D(8,0),
设AD的解析式为y=kx+b,则
|
解得k=-1,b=8.
∴AD的解析式为y=-x+8.
(3)BC=CE,
证明:过点C作CF⊥y轴,交直线AB于点F,
∵BC⊥CE,
∴∠BCE=∠ACF=90°,
∴∠BCF=∠ACE,

又∵∠OAB=∠OAD=45°,
∴∠CFA=90°-45°=∠OAD,
∴∠BAC=∠AFC,
∴CA=CF,
在△ACE和△FCB中
|
∴△ACE≌△FCB(ASA),
∴BC=CE.
其它方法一:连接CD,然后证CD=CE;方法二:过点C作CG⊥y轴,交直线AD于点G,证△ECG≌△BCA.
点评:考查了一次函数综合题,涉及的知识点有:坐标轴上点的特征,全等三角形的判定和性质,待定系数法求直线的函数关系式,等腰直角三角形的性质,综合性较强,有一定的难度.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列说法中,错误的是( )
| A、四个角都相等的四边形是矩形 |
| B、每组邻边都相等的四边形是菱形 |
| C、对角线互相垂直的平行四边形是正方形 |
| D、对角线互相平分的四边形是平行四边形 |
 如图,已知直线AB∥CD,∠ABE=60°,∠CDE=20°,求∠BED的度数.
如图,已知直线AB∥CD,∠ABE=60°,∠CDE=20°,求∠BED的度数.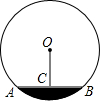 如图,AB是⊙O的弦,OC⊥AB于C,且OC=
如图,AB是⊙O的弦,OC⊥AB于C,且OC=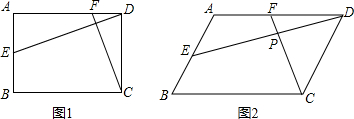
 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与函数
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与函数