题目内容
已知一个六位自然数
是99的倍数(其中x、y是阿拉伯数字),试求950x+24y+1= .
. |
| 13xy54 |
考点:数的十进制
专题:
分析:由题意可知六位自然数
能被9,11整除,根据整数能被9,11整除的性质求出x,y的值.
. |
| 13xy54 |
解答:解:因为
是99的倍数,而99=9×11,
所以 9|
,11|
,
即有:(1)9|(1+3+5+4+x+y)9|x+y+4,
而 4≤x+y+4≤22,
故 x+y+4=9或x+y+4=18,
即 x+y=5或x+y=14,
(2)11|(4+y+3-1-x-5),
即 11|y-x+1,
而-8≤y-x+1≤10,
即 y-x+1=0,
由(1),(2)得
或
解得:
,
故950x+24y+1=950×3+24×2+1=2899.
故答案为:2899.
. |
| 13xy54 |
所以 9|
. |
| 13xy54 |
. |
| 13xy54 |
即有:(1)9|(1+3+5+4+x+y)9|x+y+4,
而 4≤x+y+4≤22,
故 x+y+4=9或x+y+4=18,
即 x+y=5或x+y=14,
(2)11|(4+y+3-1-x-5),
即 11|y-x+1,
而-8≤y-x+1≤10,
即 y-x+1=0,
由(1),(2)得
|
|
解得:
|
故950x+24y+1=950×3+24×2+1=2899.
故答案为:2899.
点评:此题主要考查了数的十进制,利用能被9整除的数的特点:各位数字之和能被9整除,则该数能被9整除;能被11整除的数的特点:奇数位的数字和与偶数位的数字和的差能被11整除,则该数能被11整除,进而得出是解题关键.

练习册系列答案
相关题目
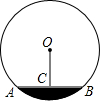 如图,AB是⊙O的弦,OC⊥AB于C,且OC=
如图,AB是⊙O的弦,OC⊥AB于C,且OC= 已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与函数
已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与函数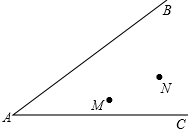 如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且使PM=PN,请你通过尺规作图找出这一P点,(不写作法,保留作图痕迹).
如图,两个班的学生分别在M、N两处参加植树劳动,现要在道路AB、AC的交叉区域内设一个茶水供应点P,使P到两条道路的距离相等,且使PM=PN,请你通过尺规作图找出这一P点,(不写作法,保留作图痕迹). 已知:DC∥AB,AC平分∠DAB
已知:DC∥AB,AC平分∠DAB 如图,△ABC中,∠C=90°,若a+b=17,c=13,则△ABC的面积是
如图,△ABC中,∠C=90°,若a+b=17,c=13,则△ABC的面积是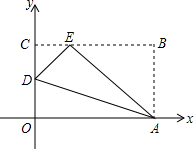 如图,OABC是一张放在平面直角坐标系中的长方形纸片.O为原点,OA=10,OC=8,在OC上取一点D,将纸片沿AD折叠使点O落在BC边上的点E处,则D、E的坐标分别是
如图,OABC是一张放在平面直角坐标系中的长方形纸片.O为原点,OA=10,OC=8,在OC上取一点D,将纸片沿AD折叠使点O落在BC边上的点E处,则D、E的坐标分别是