题目内容
17. 如图,△ABC中,DE,GF分别是AC,BC的垂直平分线,AD⊥CD,AD=4,BG=5.则△ABC的面积等于24.
如图,△ABC中,DE,GF分别是AC,BC的垂直平分线,AD⊥CD,AD=4,BG=5.则△ABC的面积等于24.
分析 连接CG,根据相等垂直平分线的性质得到CD=AD=4,CG=BG=5,根据勾股定理得到DG=$\sqrt{C{G}^{2}-C{D}^{2}}$=3,由三角形的面积公式即可得到结论.
解答 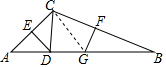 解:连接CG,
解:连接CG,
∵DE,GF分别是AC,BC的垂直平分线,
∴CD=AD=4,CG=BG=5,
∵AD⊥CD,
∴DG=$\sqrt{C{G}^{2}-C{D}^{2}}$=3,
∴AB=AD+DG+BG=12,
∴△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×12×4=24,
故答案为:24.
点评 本题考查了相等垂直平分线的性质,勾股定理,三角形的面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5.已知:x-2y=-3,则代数式(2y-x)2-2x+4y-1的值为( )
| A. | 2 | B. | 14 | C. | -4 | D. | 0 |
9.去年,中央财政安排资金11200000000元,免除城市义务教育学生学杂费,支持进城务工人员随迁子女接受义务教育,这个数据用科学记数法表示为( )
| A. | 1.1×1011 | B. | 1.12×1010 | C. | 1.12×1011 | D. | 112×108 |
7.已知点P(3,-2),则点P位于平面直角坐标系中的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
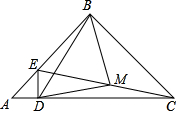 已知在△ABC中,∠ABC=90°,AB=BC=8cm,点D为AC一点,过点D作DE⊥AC交线段AB于点E,点M为EC的中点.
已知在△ABC中,∠ABC=90°,AB=BC=8cm,点D为AC一点,过点D作DE⊥AC交线段AB于点E,点M为EC的中点.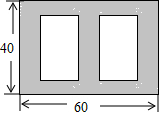 如图,在长60m,宽40m的长方形花园中,欲修宽度相等的观赏路(图中阴影部分),要使观赏路面积占总面积的$\frac{7}{16}$,求观赏路面宽是多少m.
如图,在长60m,宽40m的长方形花园中,欲修宽度相等的观赏路(图中阴影部分),要使观赏路面积占总面积的$\frac{7}{16}$,求观赏路面宽是多少m. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.