题目内容
6. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,点B所经过的路径的长度.
分析 (1)先利用点A、B的坐标画出直角坐标系,再利用网格特点和旋转的性质画出点A1、B1,从而得到写出点A1、B1的坐标;
(2)点B所经过的路径为以B点为圆心,BC为半径,圆心角为90°的弧,然后利用弧长公式计算即可.
解答 解:(1)如图,△A1B1C为所作,点A1、B1的坐标分别为(4,3),(4,1);
(2)点B所经过的路径的长度=$\frac{90•π•3}{180}$=$\frac{3}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
16.要使分式$\frac{2x-3}{x-2}$的值存在(有意义),x的取值范围是( )
| A. | x=2 | B. | x≠2 | C. | $x=\frac{3}{2}$ | D. | $x≠\frac{3}{2}$ |
18.下列运算正确的是( )
| A. | m6÷m2=m4 | B. | (-2a2bc)3=8a6b3c3 | C. | (m3)4=m7 | D. | (2a3+a2)÷a2=3a3 |
15.在一次抗震救灾中,某市组织20辆汽车装运食品、药品、生活用品三种救灾物资到灾民安置区,按计划每辆汽车只能装运一种救灾物资且必须装满.已知用了a辆汽车装运食品,用了b辆汽车装运药品,其余剩下的汽车装运生活用品,根据表中提供的信息,解答下列问题:
(1)20辆汽车共装载了多少吨救灾物资?
(2)装运这批救灾物资的总费用是多少元?
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载(吨) | 6 | 5 | 4 |
| 每吨所需运费(元) | 120 | 160 | 100 |
(2)装运这批救灾物资的总费用是多少元?
 如图,△ABC中,DE,GF分别是AC,BC的垂直平分线,AD⊥CD,AD=4,BG=5.则△ABC的面积等于24.
如图,△ABC中,DE,GF分别是AC,BC的垂直平分线,AD⊥CD,AD=4,BG=5.则△ABC的面积等于24.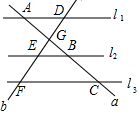 如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,直线a、b交于点G,若BC=3BG,AG=2,BG=3,则DE:EF=5:9.
如图,l1∥l2∥l3,直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,直线a、b交于点G,若BC=3BG,AG=2,BG=3,则DE:EF=5:9.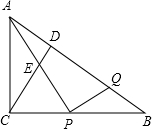 如图,Rt△ABC中,CD为斜边AB上的高,P为BC边上一点(不与B、C重合),过点P作PQ⊥AP交AB于Q,连接AP交CD于点E.
如图,Rt△ABC中,CD为斜边AB上的高,P为BC边上一点(不与B、C重合),过点P作PQ⊥AP交AB于Q,连接AP交CD于点E. 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中A点的坐标为(-3,0).
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中A点的坐标为(-3,0).