题目内容
7.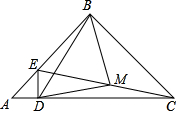 已知在△ABC中,∠ABC=90°,AB=BC=8cm,点D为AC一点,过点D作DE⊥AC交线段AB于点E,点M为EC的中点.
已知在△ABC中,∠ABC=90°,AB=BC=8cm,点D为AC一点,过点D作DE⊥AC交线段AB于点E,点M为EC的中点.(1)求证:△BMD为等腰直角三角形;
(2)当AD为$\sqrt{2}$cm,求四边形BEDM的面积.
分析 (1)根据直角三角形斜边上的中线等于斜边的一半可得BM=$\frac{1}{2}$CE,DM=$\frac{1}{2}$CE,得出BM=DM,再由等腰三角形的性质和三角形的外角性质证出∠BMD=90°即可;
(2)过B作BF⊥DE交DE的延长线于F,推出△BEF是等腰直角三角形,根据勾股定理得到AE=$\sqrt{2}$AD=2cm,BF=3$\sqrt{2}$cm,CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=10cm,根据三角形的面积即刻得到结论.
解答 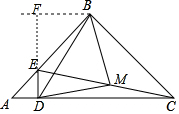 (1)证明:∵DE⊥AC,
(1)证明:∵DE⊥AC,
∴∠EDC=90°,
∵∠ABD=90°,点M为EC的中点,
∴DM=BM=CM,
∴∠MBC=∠BCM,∠MCD=∠MDC,
∵∠BME=∠MBC+∠BCM,∠DME=∠MCD+∠MDC,
∴∠BMD=∠BME+∠DME=2∠ACB=90°,
∴△BMD为等腰直角三角形;
(2)过B作BF⊥DE交DE的延长线于F,
∵∠ADE=90°,∠A=45°,
∴∠FEB=∠AED=45°,
∴△BEF是等腰直角三角形,
∵AD=$\sqrt{2}$cm,∴AE=$\sqrt{2}$AD=2cm,
∴BE=6cm,∴BF=3$\sqrt{2}$cm,
∴CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=10cm,
∴DM=BM=5cm,
∴四边形BEDM的面积=S△BEM+S△BDE=$\frac{1}{2}×$5×5+$\frac{1}{2}$×$\sqrt{2}$×3$\sqrt{2}$=15.5cm2.
点评 本题考查了等腰直角三角形的判定和性质,直角三角形的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.下列计算正确的是( )
| A. | $\sqrt{2}$$+\sqrt{2}$=2 | B. | 3+$\sqrt{2}$=3$\sqrt{2}$ | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{9}$+$\sqrt{3}$=3$+\sqrt{3}$ |
16.要使分式$\frac{2x-3}{x-2}$的值存在(有意义),x的取值范围是( )
| A. | x=2 | B. | x≠2 | C. | $x=\frac{3}{2}$ | D. | $x≠\frac{3}{2}$ |
 太极图的形状为阴阳两鱼互纠在一起(如图),象征两极和合.太极图中的白色部分作怎样的变换,可得到黑色部分?若整个圆的直径为6cm,求出图中黑色部分的面积?
太极图的形状为阴阳两鱼互纠在一起(如图),象征两极和合.太极图中的白色部分作怎样的变换,可得到黑色部分?若整个圆的直径为6cm,求出图中黑色部分的面积?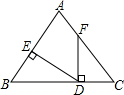 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF=50°.
如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF=50°. 如图,△ABC中,DE,GF分别是AC,BC的垂直平分线,AD⊥CD,AD=4,BG=5.则△ABC的面积等于24.
如图,△ABC中,DE,GF分别是AC,BC的垂直平分线,AD⊥CD,AD=4,BG=5.则△ABC的面积等于24.