题目内容
10.已知直线l的解析式为y=kx+3,与y轴交于点A,点C在x轴上,AC=$\sqrt{10}$.将线段AC绕点C逆时针旋转90°得到线段BC,若点B在直线l上,则k的值为$\frac{1}{2}$.分析 根据题意画出图形,如图所示,由A坐标与AC的长,求出C坐标,设B(x,kx+3),利用两点间的距离公式表示出AB2与BC2,消去x求出k的值即可.
解答  解:由题意可得:A(0,3),AC=$\sqrt{10}$,
解:由题意可得:A(0,3),AC=$\sqrt{10}$,
∴C(-1,0),
设B(x,kx+3),
∴BC=$\sqrt{10}$,
∵∠ACB=90°,
∴AB=2$\sqrt{5}$,
综上可得:AB2=x2+(kx+3-3)2=20,BC2=(x+1)2+(kx+3)2=10,
∴(k2+1)x2=20,x[(k2+1)x+(2+6k)]=0,
∵x≠0,
∴x=-$\frac{6k+2}{{k}^{2}+1}$,
∴$\frac{(6k+2)^{2}}{({k}^{2}+1)^{2}}$•(k2+1)=20,
整理得:(2k-1)(k+2)=0,
∵k>0,
∴k=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了坐标与图形变化-旋转,以及一次函数图象上点的坐标特征,灵活运用两点间的距离公式是解本题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
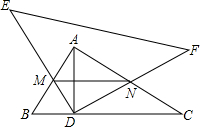 如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC上的高,另有一Rt△DEF(其直角顶点在D点)绕D点旋转,在旋转过程中,DE,DF分别与边AB,AC交于M、N点,则线段MN的最小值为$\frac{24}{5}$.
如图,Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC上的高,另有一Rt△DEF(其直角顶点在D点)绕D点旋转,在旋转过程中,DE,DF分别与边AB,AC交于M、N点,则线段MN的最小值为$\frac{24}{5}$.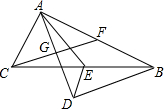 如图,Rt△ABC中,∠BAC=90°,点E是BC的中点,AD平分∠BAC,BD⊥AD于点D.
如图,Rt△ABC中,∠BAC=90°,点E是BC的中点,AD平分∠BAC,BD⊥AD于点D.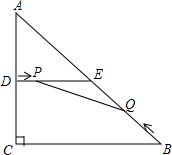 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.当S△PQE:S△ABC=1:40时,求运动时间t.
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,D、E分别是AC、AB的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s.当S△PQE:S△ABC=1:40时,求运动时间t.
 在平面直角坐标系中,长方形ABCD的边BC∥x轴,若A点的坐标为(-1,2$\sqrt{2}$),C点坐标为(3,-2$\sqrt{2}$).
在平面直角坐标系中,长方形ABCD的边BC∥x轴,若A点的坐标为(-1,2$\sqrt{2}$),C点坐标为(3,-2$\sqrt{2}$).