题目内容
18.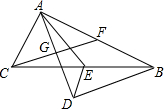 如图,Rt△ABC中,∠BAC=90°,点E是BC的中点,AD平分∠BAC,BD⊥AD于点D.
如图,Rt△ABC中,∠BAC=90°,点E是BC的中点,AD平分∠BAC,BD⊥AD于点D.(1)求证:∠ADE=∠BDE.
(2)过点C作CG⊥AD于点G,交AB于点F,求证:DE=$\frac{1}{2}BF$.
分析 (1)由AD平分∠BAC可以得出∠DAB=$\frac{1}{2}$∠BAC=45°,由BD⊥AD可以得出∠ADB=90°,就有∠DBA=∠DAB=45°,得出AD=BD,再通过证明△AED≌△BED就可以得出结论;
(2)作EH∥CF交AB于H,由CE=BE,得出FH=BH=$\frac{1}{2}$BF,根据EH∥BD,∠BDE=∠ABD=45°,证得四边形BDEH是等腰梯形,得出DE=BH,从而证得结论.
解答 (1)证明:∵Rt△ABC中,∠BAC=90°,点E是BC的中点,
∴AE=BE,
∵AD平分∠BAC,
∴∠CAD=∠BAD=45°,
∵BD⊥AD,
∴∠ABD=45°,
∴∠BAD=∠ABD,
∴AD=BD,
在△ADE和△BDE中,
$\left\{\begin{array}{l}{AD=BD}\\{DE=DE}\\{AE=BE}\end{array}\right.$,
∴△ADE≌△BDE(SSS),
∴∠ADE=∠BDE;
(2)解:如图,作EH∥CF交AB于H,
∵CE=BE,
∴FH=BH=$\frac{1}{2}$BF,
∵AG⊥AD,BD⊥AD,
∴CF∥BD,
∴EH∥BD,
∵∠BDE=∠ABD=45°,
∴四边形BDEH是等腰梯形,
∴DE=BH,
∴DE=$\frac{1}{2}$BF.
点评 本题考查了角平分线的性质,三角形全等的判定和性质,平行线的判定和性质,等腰梯形的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
11.计算a6b2÷(ab)2的结果是( )
| A. | a3 | B. | a4 | C. | a3b | D. | a4b |
13.某批发商欲将一批水产品委托货运公司由A 地运往B地销售,已知A、B两地相距120km,货运车辆的平均速度是60km/h.货运公司的收费项目及收费标准如下表:
(1)若该批发商有x t水产品要运输,货运公司收取的总费用为y元,写出y与x之间的函数表达式.
(2)如果该批发商想运送5t水产品,支付运费1500元,货运公司愿意运送这批水产品吗?
| 运输量单价[元/(吨•千米)] | 冷藏费单价[元/(吨•时)] | 过路过桥费(元) |
| 2 | 5 | 200 |
(2)如果该批发商想运送5t水产品,支付运费1500元,货运公司愿意运送这批水产品吗?
7.我市常乐镇A、B两村盛产草莓,A村有草莓200吨,B村有草莓300吨,现将这些草莓运到C、D两个冷藏仓库,已知C仓库可储存240吨,D仓库可储存260吨,从A村运往C、D两处的费用分别为每吨20元和25元,从B村运往C、D两处的费用分别为每吨15元和18元.设从A村运往C仓库的草莓重量为x吨,A、B两村运往两仓库的草莓运输费用分别为yA元和yB元.
(1)请填写下表
(2)求出yA、yB与x之间的函数解析式;
(3)考虑B村的经济承受能力,B村的草莓运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?并求出这个最小值.
(1)请填写下表
| 收地 运地 | C | D | 总计(吨) |
| A | x | 200-x | 200 |
| B | 240-x | x+60 | 300 |
| 总计(吨) | 240 | 260 | 500 |
(3)考虑B村的经济承受能力,B村的草莓运费不得超过4830元,在这种情况下,请问怎样调运才能使两村运费之和最小?并求出这个最小值.
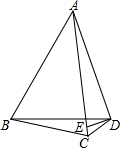 如图,四边形ABCD中,AC、BD是对角线,AB=AC,∠ABD=60°,过D作ED⊥AD,交AC于点E,恰有DE平分∠BDC.试判断线段CD、BD与AC之间有怎样的数量关系?并证明你的结论.
如图,四边形ABCD中,AC、BD是对角线,AB=AC,∠ABD=60°,过D作ED⊥AD,交AC于点E,恰有DE平分∠BDC.试判断线段CD、BD与AC之间有怎样的数量关系?并证明你的结论.