题目内容
老师讲完“一次函数”这节课后,让同学们讨论下列问题:
(1)x从0开始逐渐增大时,y=2x+8和y=6x哪一个的函数值先达到30?这说明了什么?
(2)直线y=-x与y=-x+6的位置关系如何?
甲生说:“y=6x的函数值先达到30,说明y=6x比y=2x+8的值增长得快.”
乙生说:“直线y=-x与y=-x+6是互相平行的.”
你认为这两个同学的说法正确吗?
(1)x从0开始逐渐增大时,y=2x+8和y=6x哪一个的函数值先达到30?这说明了什么?
(2)直线y=-x与y=-x+6的位置关系如何?
甲生说:“y=6x的函数值先达到30,说明y=6x比y=2x+8的值增长得快.”
乙生说:“直线y=-x与y=-x+6是互相平行的.”
你认为这两个同学的说法正确吗?
考点:一次函数的性质
专题:阅读型
分析:(1)先令y=30,求出x的值即可得出结论;
(2)根据(1)中的结论可知甲的结论正确,再由直线y=-x与y=-x+6的斜率相同可知两直线平行.
(2)根据(1)中的结论可知甲的结论正确,再由直线y=-x与y=-x+6的斜率相同可知两直线平行.
解答:解:(1)令y=30,
∵当2x+8=30时,解得x=11;
当6x=30时,x=5,
∴函数y=6x先达到30,
∴斜率大的函数函数值增长较快;
(2)甲乙的说法均正确.
∵由(1)可知y=6x的函数值先达到30,
∴甲的说法正确.
∵直线y=-x与y=-x+6的斜率相同,
∴两线互相平行.
∵当2x+8=30时,解得x=11;
当6x=30时,x=5,
∴函数y=6x先达到30,
∴斜率大的函数函数值增长较快;
(2)甲乙的说法均正确.
∵由(1)可知y=6x的函数值先达到30,
∴甲的说法正确.
∵直线y=-x与y=-x+6的斜率相同,
∴两线互相平行.
点评:本题考查的是一次函数的性质,熟知一次函数的增减性与系数k的关系是解答此题的关键.

练习册系列答案
相关题目
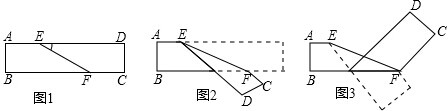

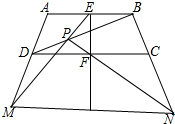 如图,已知四边形ABCD,E是AB中点,F是CD中点,P是BD对角线上一点,EP延长线交AD延长线于点M,PF延长线交BC延长线于点N,证明:直线EF平分MN.
如图,已知四边形ABCD,E是AB中点,F是CD中点,P是BD对角线上一点,EP延长线交AD延长线于点M,PF延长线交BC延长线于点N,证明:直线EF平分MN.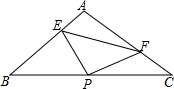 如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.
如图Rt△ABC中,AB=AC=2,P是斜边BC中点,∠EPF两边分别交边AB、AC于E、F,且AF=BE.