题目内容
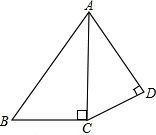 如图,已知:∠ACB=∠ADC=90°,AD=2,CD=
如图,已知:∠ACB=∠ADC=90°,AD=2,CD=| 2 |
考点:相似三角形的判定
专题:
分析:首先利用勾股定理求出AC的长,再根据如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.在Rt△ABC和Rt△ACD,直角边的对应需分情况讨论即可.
解答:解:∵AD=2,CD=
,
∴AC=
=
.
要使这两个直角三角形相似,有两种情况:(1)当Rt△ABC∽Rt△ACD时,有
=
,∴AB=3;
(2)当Rt△ACB∽Rt△CDA时,有
=
,∴AB=3
.
即当AB的长为3或3
时,这两个直角三角形相似.
故答案为:3或3
.
| 2 |
∴AC=
22+(
|
| 6 |
要使这两个直角三角形相似,有两种情况:(1)当Rt△ABC∽Rt△ACD时,有
| AC |
| AD |
| AB |
| AC |
(2)当Rt△ACB∽Rt△CDA时,有
| AC |
| CD |
| AB |
| AC |
| 2 |
即当AB的长为3或3
| 2 |
故答案为:3或3
| 2 |
点评:本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为( )| A、1 | B、2 | C、3 | D、4 |
 如图△ABC中,DE∥BC,AD=2,BD=3,BC=6,则DE=
如图△ABC中,DE∥BC,AD=2,BD=3,BC=6,则DE= 如图,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,若以“SAS”为依据,补充的条件是
如图,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,若以“SAS”为依据,补充的条件是

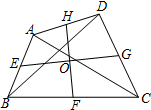 如图,在四边形ABCD中,AC=BD=3,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=
如图,在四边形ABCD中,AC=BD=3,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=