题目内容

已知圆心角为120°的扇形的面积为12πcm2，则扇形的弧长是
 
cm．
考点：扇形面积的计算,弧长的计算
专题：
分析：根据扇形面积公式S=
nπR2
360
 和弧长公式l=
nπr
180
进行计算．
解答：解：令扇形的半径和弧长分别为R和l，则
∵S=
120πR2
360
=12π，
∴R=6cm，
∴l=
120π6
180
=4πcm．
∴扇形的弧长为4πcm．
点评：本题考查了弧长的计算和扇形面积的计算．解答该题需要牢记弧长公式和扇形的面积公式．
练习册系列答案
相关题目
如图，幼儿园计划用20米的围栏靠墙围成一个小矩形花园ABCD．设AB=x，矩形的面积为S平方米．那么x为多少时，S的值最大？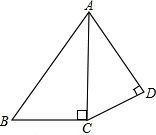
如图，已知：∠ACB=∠ADC=90°，AD=2，CD=
2
，当AB的长为
 
时，△ACB与△ADC相似．
在△ABC和△DEF中，已知∠A=∠D，AB=4，AC=3，DE=1，当DF等于
 
时，△ABC和△DEF相似．
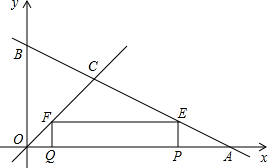如图，直线y=-x+8与坐标轴分别交于点A、B，与直线y=x交于点C．在线段OA上，动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动，同时动点P从点A出发向点O做匀速运动，当点P、Q其中一点停止运动时，另一点也停止运动．分别过点P、Q作x轴的垂线，交直线AB、OC于点E、F，连接EF．若运动时间为t秒，在运动过程中四边形PEFQ总为矩形（点P、Q重合除外）．
（1）求点P运动的速度是多少？
（2）当t为多少秒时，矩形PEFQ为正方形？
（3）当t为多少秒时，矩形PEFQ的面积S最大？并求出最大值．
计算3-2正确的是（　　）
A、-
1
9
B、
1
9
C、
1
6
D、-
1
6
如图，从下列四个条件∠1+∠2=180°、∠2=∠3、∠1+∠3=180°、l1∥l2中选一个作为题设，一个作为结论，写出一个真命题为
 
．
如果收入20元记作+20元，那么-75元表示（　　）
A、收入75元
B、收入-75元
C、支出75元
D、支出-75元
下列图形中具有稳定性的是（　　）
A、六边形B、五边形
C、平行四边形D、三角形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网