题目内容
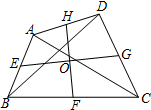 如图,在四边形ABCD中,AC=BD=3,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=
如图,在四边形ABCD中,AC=BD=3,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2=考点:中点四边形
专题:
分析:连接EF,FG,GH,EH,由E、F、G、H分别是AB、BC、CD、DA的中点,得到EH,EF,FG,GH分别是△ABD,△ABC,△BCD,△ACD的中位线,根据三角形中位线定理得到EH,FG等于BD的一半,EF,GH等于AC的一半,由AC=BD=3,得到EH=EF=GH=FG=
,根据四边都相等的四边形是菱形,得到EFGH为菱形,然后根据菱形的性质得到EG⊥HF,且EG=2OE,FH=2OH,在Rt△OEH中,根据勾股定理得到OE2+OH2=EH2=
,再根据等式的性质,在等式的两边同时乘以4,根据4=22,把等式进行变形,并把EG=2OE,FH=2OH代入变形后的等式中,即可求出EG2+FH2的值
| 3 |
| 2 |
| 9 |
| 4 |
解答: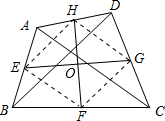 解:如右图,连接EF,FG,GH,EH,
解:如右图,连接EF,FG,GH,EH,
∵E、H分别是AB、DA的中点,
∴EH是△ABD的中位线,
∴EH=
BD=
,
同理可得EF,FG,GH分别是△ABC,△BCD,△ACD的中位线,
∴EF=GH=
AC=
,FG=
BD=
,
∴EH=EF=GH=FG=
,
∴四边形EFGH为菱形,
∴EG⊥HF,且垂足为O,
∴EG=2OE,FH=2OH,
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH2=
,
等式两边同时乘以4得:4OE2+4OH2=
×4=9,
∴(2OE)2+(2OH)2=9,
即EG2+FH2=9.
故答案为:9.
 解:如右图,连接EF,FG,GH,EH,
解:如右图,连接EF,FG,GH,EH,∵E、H分别是AB、DA的中点,
∴EH是△ABD的中位线,
∴EH=
| 1 |
| 2 |
| 3 |
| 2 |
同理可得EF,FG,GH分别是△ABC,△BCD,△ACD的中位线,
∴EF=GH=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴EH=EF=GH=FG=
| 3 |
| 2 |
∴四边形EFGH为菱形,
∴EG⊥HF,且垂足为O,
∴EG=2OE,FH=2OH,
在Rt△OEH中,根据勾股定理得:OE2+OH2=EH2=
| 9 |
| 4 |
等式两边同时乘以4得:4OE2+4OH2=
| 9 |
| 4 |
∴(2OE)2+(2OH)2=9,
即EG2+FH2=9.
故答案为:9.
点评:此题考查了菱形的判定与性质,勾股定理,三角形的中位线定理以及等式的基本性质,本题的关键是连接EF,FG,GH,EH,得到四边形EFGH为菱形,根据菱形的性质得到EG⊥HF,建立直角三角形,利用勾股定理来解决问题.

练习册系列答案
相关题目
如果收入20元记作+20元,那么-75元表示( )
| A、收入75元 |
| B、收入-75元 |
| C、支出75元 |
| D、支出-75元 |
下列图形中具有稳定性的是( )
| A、六边形 | B、五边形 |
| C、平行四边形 | D、三角形 |
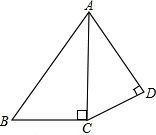 如图,已知:∠ACB=∠ADC=90°,AD=2,CD=
如图,已知:∠ACB=∠ADC=90°,AD=2,CD= 如图,从下列四个条件∠1+∠2=180°、∠2=∠3、∠1+∠3=180°、l1∥l2中选一个作为题设,一个作为结论,写出一个真命题为
如图,从下列四个条件∠1+∠2=180°、∠2=∠3、∠1+∠3=180°、l1∥l2中选一个作为题设,一个作为结论,写出一个真命题为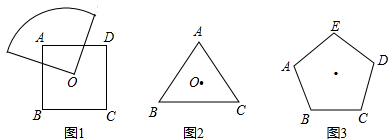
 如图,正方形的边长为2x,用整式表示图中阴影部分的面积为
如图,正方形的边长为2x,用整式表示图中阴影部分的面积为