题目内容
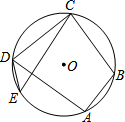
四边形ABCD内接于⊙O,CB=CD,∠A=100°,点E在
上,则∠E的度数为 .
 |
| AD |

考点:圆内接四边形的性质
专题:
分析:连接BD,先根据∠A=100°求出∠BCD的度数,再由CB=CD求出∠DBC的度数,根据圆周角定理即可得出结论.
解答: 解:∵四边形ABCD内接于⊙O,∠A=100°,
解:∵四边形ABCD内接于⊙O,∠A=100°,
∴∠BCD=180°-100°=80°.
∵CB=CD,
∴∠DBC=
=50°,
∴∠E=∠DBC=50°.
故答案为:50°.
 解:∵四边形ABCD内接于⊙O,∠A=100°,
解:∵四边形ABCD内接于⊙O,∠A=100°,∴∠BCD=180°-100°=80°.
∵CB=CD,
∴∠DBC=
| 180°-80° |
| 2 |
∴∠E=∠DBC=50°.
故答案为:50°.
点评:本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 实数a,b在数轴上对应点的位置如图所示,则下列结论正确的是( )
实数a,b在数轴上对应点的位置如图所示,则下列结论正确的是( )| A、a+b>0 | ||
| B、a-b<0 | ||
| C、ab>0 | ||
D、
|
一元二次方程x2-16=0的解是( )
| A、x1=2,x2=-2 |
| B、x1=4,x2=-4 |
| C、x1=8,x2=-8 |
| D、x1=16,x2=-16 |
 如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC的大小为( )
如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC的大小为( )| A、135° | B、120° |
| C、90° | D、60° |
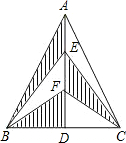 如图,△ABC中,AB=AC,AD⊥BC,点E、F是AD的三等分点,若S△ABC=12m2,则S阴影=
如图,△ABC中,AB=AC,AD⊥BC,点E、F是AD的三等分点,若S△ABC=12m2,则S阴影= 如图,在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=3,CD=2.5,则sinA=
如图,在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=3,CD=2.5,则sinA=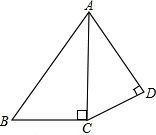 如图,已知:∠ACB=∠ADC=90°,AD=2,CD=
如图,已知:∠ACB=∠ADC=90°,AD=2,CD=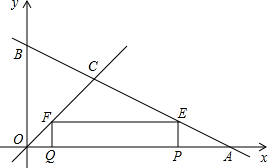 如图,直线y=-x+8与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
如图,直线y=-x+8与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).