题目内容
 如图,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,若以“SAS”为依据,补充的条件是
如图,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,若以“SAS”为依据,补充的条件是考点:全等三角形的判定
专题:
分析:先根据∠BAE=∠DAC,等号两边都加上∠EAC,得到∠BAC=∠DAE,由已知AB=AD,要使△ABC≌△ADE,根据全等三角形的判定定理ASA:添上AC=AE.
解答:解:补充的条件是:AC=AE.理由如下:
∵∠BAE=∠DAC,
∴∠BAE+∠EAC=∠DAC+∠EAC,即∠BAC=∠DAE.
∵在△ABC与△ADE中,
,
∴△ABC≌△ADE(SAS).
故答案是:AC=AE.
∵∠BAE=∠DAC,
∴∠BAE+∠EAC=∠DAC+∠EAC,即∠BAC=∠DAE.
∵在△ABC与△ADE中,
|
∴△ABC≌△ADE(SAS).
故答案是:AC=AE.
点评:本题考查了全等三角形的判定;题目是开放型题目,根据已知条件结合判定方法,找出所需条件,一般答案不唯一,只要符合要求即可.

练习册系列答案
相关题目
数轴上一点A表示-3,若将A点向左平移5个单位长度,再向右平移6个单位长度,则此时A 点表示的数是( )
| A、-1 | B、-2 | C、-3. | D、1 |
如果收入20元记作+20元,那么-75元表示( )
| A、收入75元 |
| B、收入-75元 |
| C、支出75元 |
| D、支出-75元 |
 如图,幼儿园计划用20米的围栏靠墙围成一个小矩形花园ABCD.设AB=x,矩形的面积为S平方米.那么x为多少时,S的值最大?
如图,幼儿园计划用20米的围栏靠墙围成一个小矩形花园ABCD.设AB=x,矩形的面积为S平方米.那么x为多少时,S的值最大? 如图,在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=3,CD=2.5,则sinA=
如图,在Rt△ABC中,∠C=90°,D为斜边AB的中点,AC=3,CD=2.5,则sinA=
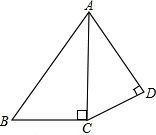 如图,已知:∠ACB=∠ADC=90°,AD=2,CD=
如图,已知:∠ACB=∠ADC=90°,AD=2,CD=