题目内容
17.如果关于x的方程x2+kx+$\frac{3}{4}$k2-3k+$\frac{9}{2}$=0的两个实数根分别为x1,x2,那么$\frac{{{x}_{1}}^{2014}}{{{x}_{2}}^{2015}}$的值为( )| A. | -1 | B. | 1 | C. | -$\frac{3}{2}$ | D. | $-\frac{2}{3}$ |
分析 先根据方程有实数根,利用根的判别式可得k2-4($\frac{3}{4}$k2-3k+$\frac{9}{2}$)≥0,求出求k的值,再把k的值代入方程,再解方程可得x1=x2=-$\frac{3}{2}$,进而可求$\frac{{{x}_{1}}^{2014}}{{{x}_{2}}^{2015}}$的值.
解答 解:根据题意可得
∵方程有实数根,
∴△=b2-4ac≥0,
即k2-4($\frac{3}{4}$k2-3k+$\frac{9}{2}$)≥0,
∴-2(k-3)2≥0,
∵(k-3)2≤0,
∴k-3=0,
即k=3,
∴原方程为:x2+3x+$\frac{9}{4}$=0,
∴x1=x2=-$\frac{3}{2}$,
∴$\frac{{{x}_{1}}^{2014}}{{{x}_{2}}^{2015}}$=($\frac{{x}_{1}}{{x}_{2}}$)2014•$\frac{1}{{x}_{2}}$=-$\frac{2}{3}$;
故选D.
点评 本题考查了根的判别式、根与系数的关系、解方程,解题的关键是根据根的判别式先求出k.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
8. 如图,已知在?ABCD中,∠B=4∠A,则∠C=( )
如图,已知在?ABCD中,∠B=4∠A,则∠C=( )
 如图,已知在?ABCD中,∠B=4∠A,则∠C=( )
如图,已知在?ABCD中,∠B=4∠A,则∠C=( )| A. | 18° | B. | 36° | C. | 45° | D. | 72° |
6.已知3是关于x的方程x2-5x+c=0的一个根,则这个方程的另一个根是( )
| A. | -2 | B. | 5 | C. | 2 | D. | 6 |
 如图,已知直线l1:y=$\frac{2}{3}$x+$\frac{8}{3}$与直线l2:y=-2x+16相交于点C,l1、l2分别交x轴于A、B两点.
如图,已知直线l1:y=$\frac{2}{3}$x+$\frac{8}{3}$与直线l2:y=-2x+16相交于点C,l1、l2分别交x轴于A、B两点. 如图,正六边形的面积为120,P是其内任意一点,求三角形PBC和三角形PEF的面积之和是多少?
如图,正六边形的面积为120,P是其内任意一点,求三角形PBC和三角形PEF的面积之和是多少?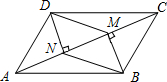 已知AC是平行四边形ABCD的一条对角线,BM⊥AC,DN⊥AC,垂足分别是M,N,求证:DM∥BN.
已知AC是平行四边形ABCD的一条对角线,BM⊥AC,DN⊥AC,垂足分别是M,N,求证:DM∥BN.