Question

2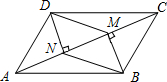．已知AC是平行四边形ABCD的一条对角线，BM⊥AC，DN⊥AC，垂足分别是M，N，求证：DM∥BN．

Answer 1

分析 欲证明DM∥BN，只要证明四边形DNBM是平行四边形即可．

解答 证明：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵DN⊥AC，BM⊥AC，
∴∠AND=∠BMC=90°，DN∥BM，
∴∠DAN=∠BCM，
在△ADN和△CBM中，
$\left\{\begin{array}{l}{∠DNA=∠BMC}\\{∠DNA=∠BMC}\\{AD=BC}\end{array}\right.$，
∴△ADN≌△BCM，
∴DN=BM．
∴四边形DNBM是平行四边形，
∴DM∥BN．

点评 本题考查平行四边形的性质，全等三角形的判定和性质等知识熟练灵活这些知识解决问题是解题的关键是，属于中考常考题型．