如图.把一张矩形纸片ABCD沿EF折叠后.点A落在CD边上的点A′处.点B落在点B′处．若∠1=115°.则∠2的度数为40°．题目和参考答案——青夏教育精英家教网—

题目内容

20．

如图，把一张矩形纸片ABCD沿EF折叠后，点A落在CD边上的点A′处，点B落在点B′处．若∠1=115°，则∠2的度数为40°．

分析根据∠1的度数，即可得到∠EFG=65°，∠EFB'=115°，进而得到∠GFB'=115°-65°=50°，再根据三角形内角和定理，即可得到∠FGB'=90°-50°=40°，最后根据对顶角相等即可得出结果．

解答解：如图，∵∠1=115°，
∴∠EFG=65°，
由折叠可得，∠EFB'=∠EFB=115°，
∴∠GFB'=115°-65°=50°，
又∵∠B'=90°，
∴∠FGB'=90°-50°=40°，
∴∠2=40°，
故答案为：40°．

点评本题主要考查了折叠问题以及平行线的性质的运用，解题时注意：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，对应边和对应角相等．

练习册系列答案

11．

某班级选派甲、乙两位同学参加学校的跳远比赛，体育老师对他们的5次训练成绩进行了整理，并绘制了不完整的统计图，如图所示，请根据图中信息，解答下列问题：
甲、乙两人跳远成绩统计表：

	第1次	第2次	第3次	第4次	第5次
甲成绩/厘米	588	597	608	610	597
乙成绩/厘米	613	618	580	a	618

根据以上信息，请解答下列问题：
（1）a=574；
（2）请完成图中表示甲成绩变化情况的折线；
（3）通过计算，补充完整下面的统计分析表；

运动员	最好成绩	平均数	众数	方差
甲	610	600	597	41.2
乙	618	600.6	618	378.24

（4）请依据（3）中所统计的数据分析，甲、乙两位同学的训练成绩各有什么特点．

a²•a⁴

a²+a⁶

（a²）⁴

a⁹-a

5．

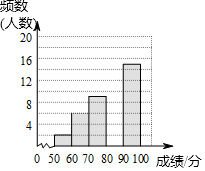为了传承中华优秀传统文化，某校组织了一次九年级350名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：

成绩x/分	频数	频率
50≤x＜60	2	0.04
60≤x＜70	6	0.12
70≤x＜80	9	b
80≤x＜90	a	0.36
90≤x＜100	15	0.30

请根据所给信息，解答下列问题：
（1）b=0.18；
（2）请补全频数分布直方图；
（3）这次比赛成绩的中位数会落在80≤x＜90分数段；
（4）若成绩在90分以上（包括90分）的为“优”等，则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人？

12．先化简再求值：$\frac{a}{a+2}$-$\frac{1}{a-1}$÷$\frac{a+2}{{a}^{2}-2a+1}$，其中a=2$\sqrt{3}$-2．

9．若$\left\{\begin{array}{l}x=2\\ y=1\end{array}$是方程组$\left\{\begin{array}{l}2ax+y=5\\ x+2y=b\end{array}$的解，则ab=4．

10．关于x的方程2x-m=1的解是x=3，则m的值为（　　）

试题分类