题目内容
15.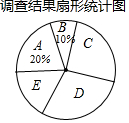 2017年全国两会民生话题成为社会焦点.徐州市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了徐州市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
2017年全国两会民生话题成为社会焦点.徐州市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了徐州市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.| 组别 | 焦点话题 | 频数(人数) |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)徐州市市区人口现有170万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
分析 (1)根据统计表中的数据可以求得本次调查的人数,从而可以求得m、n的值及扇形统计图中E组所占的百分比;
(2)根据统计表中的数据可以得到关注D组话题的市民的人数;
(3)根据统计表中的数据可以求得关注C组话题的概率.
解答 解:(1)由题意可得,
本次调查的市民有:80÷20%=400(人),
m=400×10%=40,n=400-80-40-120-60=100,
扇形统计图中E组所占的百分比为:60÷400=0.15=15%,
故答案为:40,100,15;
(2)由题意可得,
关注D组话题的市民有:170×$\frac{120}{400}$=51(万人),
答:关注D组话题的市民有51万人;
(3)由题意可得,
在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是:$\frac{100}{400}=\frac{1}{4}$,
答:在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是$\frac{1}{4}$.
点评 本题考查概率公式、用样本估计总体、统计表、扇形统计图,解答本题的关键是明确题意,找出所求问题需要的条件,利用统计图和统计表的知识解答.

练习册系列答案
相关题目
5.下列结论中不正确的是( )
| A. | 连接两点的线段叫两点之间的距离 | B. | 两点之间,线段最短 | ||
| C. | 等角的余角相等 | D. | 两点确定一条直线 |
3.下列计算正确的是( )
| A. | (-2a2)3=-8a5 | B. | a3•a2=a5 | C. | 2a2+a2=3a4 | D. | (a-b)2=a2-b2 |
5.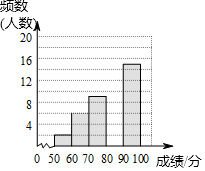 为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
请根据所给信息,解答下列问题:
(1)b=0.18;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
 为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
为了传承中华优秀传统文化,某校组织了一次九年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 2 | 0.04 |
| 60≤x<70 | 6 | 0.12 |
| 70≤x<80 | 9 | b |
| 80≤x<90 | a | 0.36 |
| 90≤x<100 | 15 | 0.30 |
(1)b=0.18;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是70°.
如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是70°.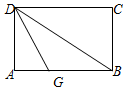 如图,将矩形纸片ABCD折叠,先折出折痕(对角线)BD,再折叠,使边DA与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是3.
如图,将矩形纸片ABCD折叠,先折出折痕(对角线)BD,再折叠,使边DA与对角线BD重合,得折痕DG,若AB=8,BC=6,则AG的长是3.