题目内容
17.已知P是反比例函数y=$\frac{1}{n(n+1)x}$图象上的点(n为正整数),过Pn作x轴的垂线,垂足为Mn,连接OPn,设△OPnMn的面积为Sn,则S1+S2+S3+…+S2015=$\frac{2015}{4032}$.分析 根据反比例函数系数k的几何意义分别表示出S1、S2、S3、…S2015,进行计算即可.
解答 解;∵P是反比例函数y=$\frac{1}{n(n+1)x}$图象上的点(n为正整数),
n=1时,y=$\frac{1}{2x}$,则S1=$\frac{1}{2}$|k|=$\frac{1}{2}$×$\frac{1}{2}$,
n=2时,y=$\frac{1}{6x}$,则S2=$\frac{1}{2}$×$\frac{1}{6}$,
n=3时,y=$\frac{1}{12x}$,则S3+=$\frac{1}{2}$×$\frac{1}{12}$,
…
n=2015时,则y=$\frac{1}{2015×2016x}$,S2015=$\frac{1}{2}$×$\frac{1}{2015×2016}$,
∴S1+S2+S3+…+S2015=$\frac{1}{2}$($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2015×2016}$)
=$\frac{1}{2}$×$\frac{2015}{2016}$
=$\frac{2015}{4032}$,
故答案为$\frac{2015}{4032}$.
点评 本题考查了反比例函数系数k的几何意义,分别表示出三角形的面积,根据代数式的规律即可求得.

练习册系列答案
相关题目
8.小明同学在计算某n边形的内角和时,不小心多输入一个内角,得到和为2005°,则n等于( )
| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
9.计算(-$\frac{1}{2}$)2016+(-$\frac{1}{2}$)2017得( )
| A. | -$\frac{1}{{2}^{2017}}$ | B. | -$\frac{1}{{2}^{2016}}$ | C. | ($\frac{1}{2}$)2017 | D. | ($\frac{1}{2}$)2016 |
 图中每个小正方形的边长都是1,已知A点可用(3,2)表示
图中每个小正方形的边长都是1,已知A点可用(3,2)表示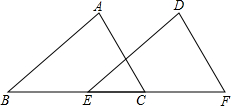 已知,如图,AC=DF,AC∥DF,BE=CF,请写出△ABC≌△DEF的理由.
已知,如图,AC=DF,AC∥DF,BE=CF,请写出△ABC≌△DEF的理由.