题目内容
1.已知一元二次方程(2k-3)x2+4kx+2k-5=0,且4k+1是腰长为7的等腰三角形的底边长,求当k取何整数时,方程有两个整数根.分析 由一元二次方程(2k-3)x2+4kx+2k-5=0有两个整数根,得出△=(4k)2-4(2k-3)(2k-5)≥0,根据三角形的三边关系得出0<4k+1<14,进一步联立不等式组求得解集,得出k的数值即可.
解答 解:∵一元二次方程(2k-3)x2+4kx+2k-5=0有两个整数根,
∴△=(4k)2-4(2k-3)(2k-5)
=64k-60≥0
解得k≥$\frac{15}{16}$
∵4k+1是腰长为7的等腰三角形的底边长,
∴0<4k+1<14,
∴-$\frac{1}{4}$<k<$\frac{13}{4}$,
∴$\frac{15}{16}$≤k<$\frac{13}{4}$,
∴k=1或2.
当k=2时,方程没有整数根,
∴k=1.
点评 此题考查一元二次方程的实际运用,掌握根的判别式和三角形的三边关系是解决问题的关键.

练习册系列答案
相关题目
13.下面是一家商店四年盈亏情况统计表:(单位:万元)
补全该表,并进一步诊断一下,该商店这四年盈利还是亏损?
| 年 | 上半年盈利 | 下半年盈利 | 算式 | 合计 |
| 第一年 | 1.2 | 0.8 | 1.2+0.8 | |
| 第二年 | -0.6 | -0.7 | (-0.6)+(-0.7) | |
| 第三年 | -0.5 | 0.5 | (-0.5)+0.5 | |
| 第四年 | 0.9 | -0.1 | 0.9+(-0.1) |
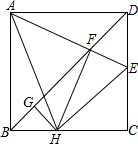 如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).
如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).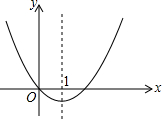 二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8.
二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8.