题目内容
12.计算:(1)(3+$\sqrt{2}$)(3-$\sqrt{2}$);
(2)(1+$\sqrt{5}$)($\sqrt{5}$-2);
(3)$\sqrt{2}$($\sqrt{2}$+8);
(4)$\sqrt{80}$×$\sqrt{5}$-$\sqrt{50}$×$\sqrt{2}$;
(5)$\frac{\sqrt{21}×\sqrt{7}}{\sqrt{3}}$;
(6)$\frac{4\sqrt{10}+5\sqrt{40}}{\sqrt{10}}$.
分析 (1)利用平方差公式求解即可;
(2)利用多项式乘多项式的方法求解;
(3)利用单项式乘多项式的方法求解;
(4)先化为最简二次根式,再利用二次根式的混合运算顺序求解即可;
(5)化为最简二次根式再利用二次根式的混合运算顺序求解即可;
(6)分子各项分别除以分母再相加即可.
解答 解:(1)(3+$\sqrt{2}$)(3-$\sqrt{2}$)
=9-2,
=7;
(2)(1+$\sqrt{5}$)($\sqrt{5}$-2)
=$\sqrt{5}$-2+5-2$\sqrt{5}$,
=3-$\sqrt{5}$;
(3)$\sqrt{2}$($\sqrt{2}$+8)=2+8$\sqrt{2}$;
(4)$\sqrt{80}$×$\sqrt{5}$-$\sqrt{50}$×$\sqrt{2}$
=4$\sqrt{5}$×$\sqrt{5}$-5$\sqrt{2}$×$\sqrt{2}$,
=20-10,
=10;
(5)$\frac{\sqrt{21}×\sqrt{7}}{\sqrt{3}}$=$\frac{7\sqrt{3}}{\sqrt{3}}$=7;
(6)$\frac{4\sqrt{10}+5\sqrt{40}}{\sqrt{10}}$
=4+10,
=14.
点评 本题主要考查了二次根式的混合运算,解题的关键是利用二次根式的性质正确的化简.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
2.下列计算正确的是( )
| A. | -3-(-2)=-1 | B. | -3-2=-1 | C. | -3÷2×2=-$\frac{3}{4}$ | D. | -(-1)2=1 |
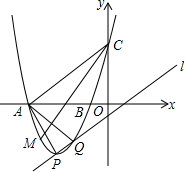 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1. 如图,CD是⊙O的直径,点E在⊙O上,AE交⊙O于点B,AB=OC,试判断∠EOD与∠A之间的数量关系并说明理由.
如图,CD是⊙O的直径,点E在⊙O上,AE交⊙O于点B,AB=OC,试判断∠EOD与∠A之间的数量关系并说明理由. 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.