题目内容
11.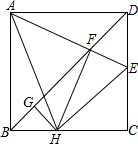 如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).
如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).
分析 ①作辅助线,延长HF交AD于点L,连接FC,通过证明△ADF≌△CDF,可得:AF=CF,故需证明FC=FH,可证:AF=FH;
②由HF⊥AP,AF=FH,可得:∠HAE=45°;
③作辅助线,连接AC交BD于点O,证BD=2FG,只需证OA=GF即可,根据△AOF≌△FGE,可证OA=GF,故可证BD=2FG;
④作辅助线,延长AD至点M,使DM=AD,过点C作CI∥FL,则IL=HC,可证AL=HF,再根据△MFC≌△MIC,可证:CI=IM,故△CEH的周长为边AM的长,为定值.
解答 解:①如图1,连接FC,延长HF交AD于点L.
∵BD为正方形ABCD的对角线,
∴∠ADB=∠CDF=45°,
∵AD=CD,DF=DF,
在△ADF与△CDF中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADF=CDF}\\{DF=DF}\end{array}\right.$
∴△ADF≌△CDF,
∴FC=AF,∠ECF=∠DAF,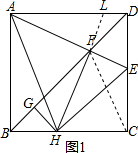
∵∠ALH+∠LAF=90°,
∴∠LHC+∠DAF=90°,
∵∠ECF=∠DAF,
∴∠FHC=∠FCH,
∴FH=FC,
∴FH=AF,故①正确;
②∵FH⊥AE,FH=AF,
∴∠HAE=45°;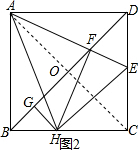 故②正确;
故②正确;
③如图2,连接AC交BD于点O,可知:BD=2OA,
∵∠AFO+∠GFH=∠GHF+∠GFH=90°,
∴∠AFO=∠GHF.
∵AF=HF,∠AOF=∠FGH=90°,
在△AOF与△FGH中,
$\left\{\begin{array}{l}{∠AFO=∠GHF}\\{AF=HF}\\{∠AOF=∠FGH}\end{array}\right.$,
∴△AOF≌△FGH,
∴OA=GF,
∵BD=2OA,
∴BD=2FG;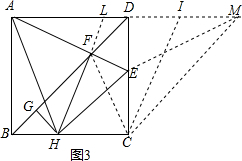 故③错误;
故③错误;
④如图3,延长AD至点M,使DM=AD,过点C作CI∥FL,则:LI=HC,
根据△MEC≌△MIC,可得:CE=IM,
同理,可得:AL=HF,
∴HP+HC+EC=AL+LI+IM=AM=8.
∴△CEH的周长为8,为定值,故④正确;
故答案为:①②④.
点评 本题考查了等腰三角形的判定和性质、全等三角形的判定和性质和正方形的性质,解答本题要充分利用正方形的特殊性质,在解题过程中要多次利用三角形全等是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | -3-(-2)=-1 | B. | -3-2=-1 | C. | -3÷2×2=-$\frac{3}{4}$ | D. | -(-1)2=1 |
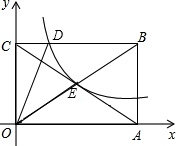 如图,反比例函数y=$\frac{k}{x}$在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4).
如图,反比例函数y=$\frac{k}{x}$在第一象限的图象经过矩形OABC对角线的交点E,与BC交于点D,若点B的坐标为(6,4). 如图,BC⊥ED,垂足为点O,∠A=28°,∠B=36°,求∠D的度数.
如图,BC⊥ED,垂足为点O,∠A=28°,∠B=36°,求∠D的度数.



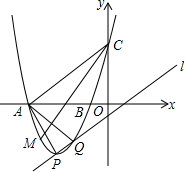 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1. 如图,CD是⊙O的直径,点E在⊙O上,AE交⊙O于点B,AB=OC,试判断∠EOD与∠A之间的数量关系并说明理由.
如图,CD是⊙O的直径,点E在⊙O上,AE交⊙O于点B,AB=OC,试判断∠EOD与∠A之间的数量关系并说明理由.