题目内容
11.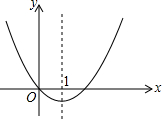 二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8.
二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8.
分析 根据对称轴求出b的值,从而得到x=-1、4时的函数值,再根据一元二次方程x2+bx-t=0(t为实数)在-1<x<4的范围内有解相当于y=x2+bx与y=t在x的范围内有交点解答.
解答  解:对称轴为直线x=-$\frac{b}{2×1}$=1,
解:对称轴为直线x=-$\frac{b}{2×1}$=1,
解得b=-2,
所以,二次函数解析式为y=x2-2x,
y=(x-1)2-1,
x=-1时,y=1+2=3,
x=4时,y=16-2×4=8,
∵x2+bx-t=0相当于y=x2+bx与直线y=t的交点的横坐标,
∴当-1≤t<8时,在-1<x<4的范围内有解.
故答案为:-1≤t<8.
点评 本题考查了二次函数与不等式,把方程的解转化为两个函数图象的交点的问题求解是解题的关键,作出图形更形象直观.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
16.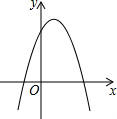 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )
已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )
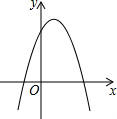 已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )
已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )| A. | 无实数根 | B. | 有两个同号不等实数根 | ||
| C. | 有两个异号实数根 | D. | 有两个相等实数根 |
 如图,CD是⊙O的直径,点E在⊙O上,AE交⊙O于点B,AB=OC,试判断∠EOD与∠A之间的数量关系并说明理由.
如图,CD是⊙O的直径,点E在⊙O上,AE交⊙O于点B,AB=OC,试判断∠EOD与∠A之间的数量关系并说明理由.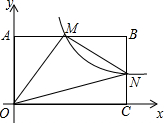 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.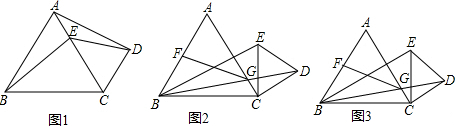
 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022. (1)在所给平面直角坐标系中,画出反比例函数y=$\frac{4}{x}$的图象;
(1)在所给平面直角坐标系中,画出反比例函数y=$\frac{4}{x}$的图象;