题目内容
11. 如图,在平面直角坐标系中,已知A(9,0),B(0,6),⊙M经过原点O及点A、B.
如图,在平面直角坐标系中,已知A(9,0),B(0,6),⊙M经过原点O及点A、B.(1)求⊙M的半径及圆心M的坐标;
(2)过点B作⊙M的切线交x轴于点C,求过点A、B、C的抛物线的解析式;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,求点N的坐标和线段OE的长.
分析 (1)根据圆周角定理∠AOB=90°得AB为⊙M的直径,则可得到线段AB的中点即点M的坐标,然后利用勾股定理计算出AB,则可确定⊙M的半径为;
(2)点B作⊙M的切线l交x轴于C,根据切线的性质得AB⊥BC,利用等角的余角相等得到∠BAO=∠CBO,然后根据相似三角形的判定方法有Rt△ABO∽Rt△BCO,可解得OC,则可求得C点坐标为,最后运用待定系数法确定抛物线的解析式;
(3)作ND⊥x轴,连结AE,易得△NOD为等腰直角三角形,再利用ND∥OB得到△ADN∽△AOB,利用相似三角形的性质可求得ND,进一步可求得OD、ON,即可确定N点坐标;由于△ADN∽△AOB,利用相似三角形的性质可求得AN,进一步可求得BN,然后利用圆周角定理得∠OBA=OEA,∠BOE=∠BAE,所以△BON∽△EAN,再利用相似比可求出NE,最后由OE=ON+NE计算即可.
解答 解:
(1)∵∠AOB=90°,
∴AB为⊙M的直径,
∵A(9,0),B(0,6),
∴OA=9,OB=6,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=3$\sqrt{13}$,
∴⊙M的半径为$\frac{3\sqrt{13}}{2}$;
∵A(9,0),B(0,6),
∴圆心M的坐标为($\frac{9}{2}$,3);
(2)点B作⊙M的切线l交x轴于C,如图1,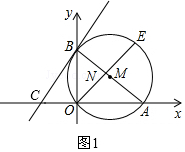
∵BC与⊙M相切,AB为直径,
∴AB⊥BC,
∴∠ABC=90°,
∴∠CBO+∠ABO=∠ABC=90°,
而∠BAO+∠ABO=90°,
∴∠BAO=∠CBO,
∴Rt△ABO∽Rt△BCO,
∴$\frac{OB}{OC}$=$\frac{OA}{OB}$,即$\frac{6}{OC}$=$\frac{9}{6}$,解得OC=4,
∴C点坐标为(-4,0),
设过A、B、C三点的抛物线解析式为y=ax2+bx+c,
把A、B、C三点的坐标代入可得$\left\{\begin{array}{l}{81a+9b+c=0}\\{16a-4b+c=0}\\{c=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{6}}\\{b=\frac{5}{6}}\\{c=6}\end{array}\right.$,
∴抛物线解析式为y=-$\frac{1}{6}$x2+$\frac{5}{6}$x+6;
(3)作ND⊥x轴,连结AE,如图2,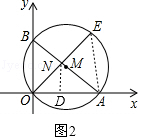
∵∠BOA的平分线交AB于点N,
∴△NOD为等腰直角三角形,
∴ND=OD,
∴ND∥OB,
∴△ADN∽△AOB,
∴ND:OB=AD:AO,
∴ND:6=(9-ND):9,解得ND=$\frac{18}{5}$,
∴OD=$\frac{18}{5}$,ON=$\sqrt{2}$ND=$\frac{18\sqrt{2}}{5}$,
∴N点坐标为($\frac{18}{5}$,$\frac{18}{5}$);
∵△ADN∽△AOB,
∴ND:OB=AN:AB,即$\frac{18}{5}$:6=AN:3$\sqrt{13}$,解得AN=$\frac{9\sqrt{13}}{5}$,
∴BN=3$\sqrt{13}$-$\frac{9\sqrt{13}}{5}$=$\frac{6\sqrt{13}}{5}$,
∵∠OBA=∠OEA,∠BOE=∠BAE,
∴△BON∽△EAN,
∴BN:NE=ON:AN,即$\frac{6\sqrt{13}}{5}$:NE=$\frac{18\sqrt{2}}{5}$:$\frac{9\sqrt{13}}{5}$,解得NE=$\frac{39\sqrt{2}}{10}$,
∴OE=ON+NE=$\frac{18\sqrt{2}}{5}$+$\frac{39\sqrt{2}}{10}$=$\frac{15\sqrt{2}}{2}$.
点评 本题为圆的综合应用,涉及切线的性质、圆周角定理及其推论、待定系数法、相似三角形的判定和性质、勾股定理等知识点.在(1)中确定出AB为直径是解题的关键,在(2)中利用相似三角形的性质求得点C的坐标是解题的关键,在(3)中构造相似三角形分别求得ON、NE的长是解题的关键.本题考查知识点较多,综合性较强,计算量大,难度很大.

| A. | a<m<n<b | B. | m<a<b<n | C. | a<m<b<n | D. | m<a<n<b |
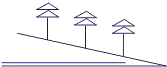 在山坡上植树,要求两棵树间的水平距离是m,测得斜坡的倾斜角为α,则斜坡上相邻两棵树的坡面距离是( )
在山坡上植树,要求两棵树间的水平距离是m,测得斜坡的倾斜角为α,则斜坡上相邻两棵树的坡面距离是( )| A. | $\frac{m}{sinα}$ | B. | $\frac{m}{cosα}$ | C. | m•tanα | D. | m•cosα |
| A. | 平方根等于本身的数是0 | |
| B. | 如果a,b都是无理数,那么a+b也一定是无理数 | |
| C. | 坐标平面内的点与有序实数对一一对应 | |
| D. | $\sqrt{12}$与6$\sqrt{\frac{1}{27}}$可以合并同类项 |
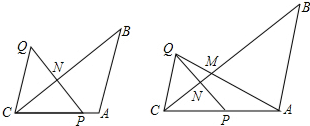

 如图所示的几何体是由7个相同的小正方体搭成的,请画出它的左视图和俯视图.
如图所示的几何体是由7个相同的小正方体搭成的,请画出它的左视图和俯视图. 已知有理数a、b在数轴上的对应的位置如图所示,化简:2|a+b|-|a-b|.
已知有理数a、b在数轴上的对应的位置如图所示,化简:2|a+b|-|a-b|.