题目内容
5.某公司生产的商品市场指导价为每千克150元,公司的实际销售价格可以浮动x个百分点(即销售价格=150(1+x%)),经过市场调研发现,这种商品的日销售量p(千克)与销售价格浮动的百分点x之间的函数关系为p=-2x+24.若该公司按浮动-12个百分点的价格出售,每件商品仍可获利10%.(1)求该公司生产销售每千克商品的成本为多少元?
(2)当该公司的商品定价为多少元时,日销售利润为576元?(说明:日销售利润=(销售价格一成本)×日销售量)
(3)该公司决定每销售一千克商品就捐赠a元利润(a≥1)给希望工程,公司通过销售记录发现,当价格浮动的百分点大于-1时,扣除捐赠后的日销售利润随x的增大而减小,直接写出a的取值范围.
分析 (1)设该公司生产销售每千克商品的成本为z元,根据该公司按浮动-12个百分点的价格出售,每千克商品仍可获利10%列出方程,求出方程的解得到z的值,即为每件商品的成本;
(2)根据日销售利润=(销售价格一成本)×日销售量,由日销售利润为576元列出关于x的方程,求出方程的解即可得到结果;
(3)根据题意得销量乘以每千克的利润等于总利润列方程,求得函数关系式W=(-2x+24)[150(1+x%)-120-a],根据二次函数的性质即可得到结论..
解答 解:(1)设该公司生产销售每千克商品的成本为z元,
依题意得:150(1-12%)=(1+10%)z,
解得:z=120,
答:该公司生产销售每千克商品的成本为120元;
(2)由题意得(-2x+24)[150(1+x%)-120]=576,
整理得:x2+8x-48=0,
解得:x1=-12,x2=4,
此时,商品定价为每件132元或156元,日销售利润为576元;
(3)则W=(-2x+24)[150(1+x%)-120-a]=-3x2+(-24+2a)x+720-24a,
∵对称轴为x=-$\frac{-24+2a}{-6}$,
∵当价格浮动的百分点大于-1时,扣除捐赠后的利润随x的增大而减小,
∴x=-$\frac{-24+2a}{-6}$≤-1,
解得:a≤9,
∵a≥1,
∴a的取值范围:1≤a≤9.
点评 此题考查了一元二次方程的应用以及二次函数的应用,弄清题意是解本题的关键.

练习册系列答案
相关题目
15.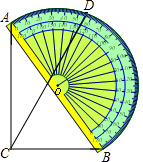 如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
 如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )| A. | 63° | B. | 54° | C. | 36° | D. | 27° |
 如图,
如图,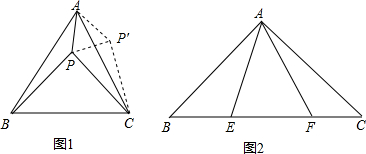
 如图,点P在∠AOB内.
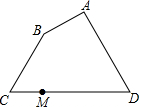
如图,点P在∠AOB内. 在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为7.
在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为7.