题目内容
11.不等式$\frac{3}{x}<4-x$的解集为1<x<3.分析 设y=$\frac{3}{x}$,y=4-x,联立方程组求出x,y的对应值,即可得到结论.
解答 解:设y=$\frac{3}{x}$,y=4-x,
解$\left\{\begin{array}{l}{y=\frac{3}{x}}\\{y=4-x}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=3}\\{{y}_{2}=1}\end{array}\right.$,
∴不等式$\frac{3}{x}<4-x$的解集为:1<x<3,
故答案为:1<x<3.
点评 本题考查的是反比例函数与一次函数的交点问题,解答此题的关键是联立关于x、y的二元一次方程组,求出x、y的对应值.

练习册系列答案
相关题目
20.某校足球比篮球数的2倍多3个,足球数与篮球数的比为3:2,求两种球各有多少.若设足球有x个,篮球有y个,由题意得( )
| A. | $\left\{\begin{array}{l}{x=2y-1}\\{2y=3x}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2y+3}\\{3x=2y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2y-3}\\{3x=2y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2y+3}\\{2x=3y}\end{array}\right.$ |
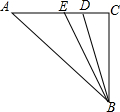 如图,在Rt△ABC中,∠C=90°,∠A=45°,BE是△ABD的角平分线,若∠DBC=15°,则∠EBD的度数为7.5°.
如图,在Rt△ABC中,∠C=90°,∠A=45°,BE是△ABD的角平分线,若∠DBC=15°,则∠EBD的度数为7.5°.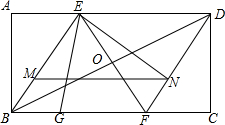 已知如图,矩形ABCD的对角线BD的中垂线分别交AD、BC边于点E、F,连结EB、DF.AB=$\sqrt{3}$,AD=3.
已知如图,矩形ABCD的对角线BD的中垂线分别交AD、BC边于点E、F,连结EB、DF.AB=$\sqrt{3}$,AD=3. 某中学为了了解七年级600名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
某中学为了了解七年级600名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题: