题目内容
2.(1)已知|a|=4,|b|=3,且a+b>0,求a-b的值.(2)已知|a|=4,b=3,求ab-5的值.
分析 (1)由绝对值的性质先求得a、b的值,然后根据a+b>0,确定出a、b的具体情况,然后再进行计算即可;
(2)先求得a、b的值,然后再进行计算即可.
解答 解:(1)∵|a|=4,|b|=3,
∴a=±4,b=±3.
又∵a+b>0,
∴a=4,b=3,或a=4,b=-3.
当a=4,b=3时,a-b=4-3=1;
当a=4,b=-3时,a-b=4-(-3)=4+3=7.
(2)∵|a|=4,
∴a=±4.
当a=4,b=3时,ab-5=4×3-5=12-5=7;
当a=-4,b=3时,ab-5=-4×3-5=-12-5=-17.
点评 本题主要考查的是绝对值的性质、有理数的混合运算,分类讨论是解题的关键.

练习册系列答案
相关题目
13.一个正方形的边长是$\frac{3}{5}$米,它的周长是( )米.
| A. | $\frac{9}{25}$ | B. | $\frac{12}{5}$ | C. | $\frac{9}{10}$ | D. | $\frac{9}{5}$ |
12.下列方程是一元二次方程的是( )
| A. | x2+3y-5=0 | B. | $\frac{1}{x}$-2x2+1=0 | ||
| C. | ax2+bx+c=0(其中a、b、c为常数) | D. | $\sqrt{3}$x2+4x-5=0 |
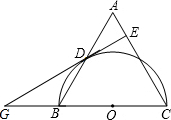 如图,△ABC中,CA=CB,以BC为直径的半圆O交于AB于D,DE⊥AC于E.求证:DE是半圆O的切线.
如图,△ABC中,CA=CB,以BC为直径的半圆O交于AB于D,DE⊥AC于E.求证:DE是半圆O的切线.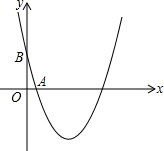 如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)
如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)