题目内容
16.满足条件$\left\{\begin{array}{l}{x+2y<\frac{x}{2}<2x+y}\\{x-3y=1}\end{array}\right.$的x的取值范围是$\frac{2}{11}$<x<$\frac{2}{5}$.分析 根据题意转化为$\left\{\begin{array}{l}{x+\frac{2}{3}(x-1)<\frac{x}{2}①}\\{\frac{x}{2}<2x+\frac{1}{3}(x-1)②}\end{array}\right.$,解不等式组即可求得x的取值范围.
解答 解:由x-3y=1得,y=$\frac{1}{3}$(x-1),
由x+2y<$\frac{x}{2}$<2x+y得,
$\left\{\begin{array}{l}{x+\frac{2}{3}(x-1)<\frac{x}{2}①}\\{\frac{x}{2}<2x+\frac{1}{3}(x-1)②}\end{array}\right.$
由①得,x<$\frac{4}{7}$;
由②得,x>$\frac{2}{11}$;
所以,x的取值范围是$\frac{2}{11}$<x<$\frac{4}{7}$.
故答案为$\frac{2}{11}$<x<$\frac{4}{7}$.
点评 本题考查了不等式组的解法,解不等式组应遵循的原则:同大取大;同小取小;大小小大去中间;大大小小无解.

练习册系列答案
相关题目
 如图,已知AC⊥AD于A,BC⊥BD于B,且AD=BC.求证:AC=BD.
如图,已知AC⊥AD于A,BC⊥BD于B,且AD=BC.求证:AC=BD.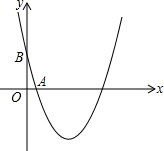 如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3)
如图,已知二次函数的图象关于x=-1对称,且最小值为-4,经过A(1,0)、B(0,-3) 已知:AB是⊙O的直径,C是AB上一点,PC⊥AB,交⊙O于F,PDE是割线,交⊙O于D、E.求证:PC2=PD•PE+AC•CB.
已知:AB是⊙O的直径,C是AB上一点,PC⊥AB,交⊙O于F,PDE是割线,交⊙O于D、E.求证:PC2=PD•PE+AC•CB.