题目内容
6.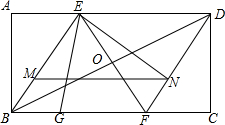 已知如图,矩形ABCD的对角线BD的中垂线分别交AD、BC边于点E、F,连结EB、DF.AB=$\sqrt{3}$,AD=3.
已知如图,矩形ABCD的对角线BD的中垂线分别交AD、BC边于点E、F,连结EB、DF.AB=$\sqrt{3}$,AD=3.(1)求DE的长.
(2)过线段BE上一点M作MN∥BC,交DF于N,在边BC上取一点G,使BG=BM,连结EG、EN,试求∠GEN的度数.
分析 (1)通过解直角△ABD得到∠ADB=30°,BD=2AB,则通过解直角△ODE来求DE边的长度;
(2)易得△EBF是等边三角形.证△EBG≌△EFN,则得∠BEG=∠FEN,可推得∠GEN=60°.
解答  解:(1)∵在直角△ABD中,AB=$\sqrt{3}$,AD=3,
解:(1)∵在直角△ABD中,AB=$\sqrt{3}$,AD=3,
∴tan∠ADB=$\frac{AB}{AD}$=$\frac{\sqrt{3}}{3}$,则∠ADB=30°,
∴BD=2AB=2$\sqrt{3}$,
又∵EF是BD的中垂线,
∴∠EOD=90°,OD=$\sqrt{3}$,
∴DE=$\frac{OD}{cos30°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$=2,即DE=2.
(2)∵四边形ABCD是矩形,
∴AD∥BC,即ED∥BF.
∴∠EDO=∠FBO.
在△EDO与△FBO中,
$\left\{\begin{array}{l}{∠EDO=∠FBO}\\{OD=OB}\\{∠EOD=∠FOB}\end{array}\right.$,
∴△EDO≌△FBO(ASA),
∴ED=FB,
∴四边形BEDF是平行四边形.
∴BE∥FD,则BM∥FN,
又∵MN∥BC,
∴四边形BMNF是平行四边形,
∴BM=FN,
又∵BG=BM,
∴BG=FN.
由(1)知,∠ADB=30°,则易得∠DEO=60°.
∴∠BEF=∠DEF=60°,
∴△EBF是等边三角形.
∴∠EBF=60°,BE=FE,
易得∠EFD=60°,即∠EFN=60°.
在△EBG与△EFN中,
$\left\{\begin{array}{l}{BE=FE}\\{∠BEG=∠EFN=60°}\\{BG=FN}\end{array}\right.$,
∴△EBG≌△EFN(SAS),
∴∠BEG=∠FEN,
∴∠GEN=∠BEF=60°.
点评 本题考查了四边形综合题.解题时,要熟练掌握全等三角形的判定与性质,矩形的性质,平行四边形的判定与性质以及正三角形的判定与性质.解答(2)题时,要利用图中相关角与角间的和差关系来求得∠GEN的度数.

| 周数x | 1 | 2 | 3 | 4 |
| 价格y1(元/桶) | 60 | 59 | 58 | 57 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出9月份y1与x的函数关系式;并求出10月份y2与x的函数关系式.
(2)若9月份该品牌的食用油进价m1(元/桶)与周数x满足函数关系为:m1=$\frac{1}{3}$x2-3x+50,10月份该品牌的食用油进价m2(元/桶)与周数x满足函数关系为:m2=$\frac{7}{2}$x+$\frac{81}{2}$,试问在9月份和10月份中,哪月的哪一周销售一桶该品牌的食用油利润最大?最大利润是多少?
(3)在第(2)问的条件下,该批发商在10月份的第2周以该周的进价购入该品牌食用油1200桶,准备在10月份第3周进行销售.在第3周以该周的销售价销售了3a%后,为了加快销售的进度,该批发商决定在原销售价格的基础上降价a%进行销售,这样顺利的完成了第三周销售1200桶的任务,且获利12000元,请你参考以下数据,估算出a的整数值(0<a<15).
(参考数据:912=8281,922=9464,932=8649,942=8836)
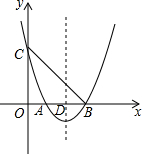 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.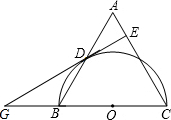 如图,△ABC中,CA=CB,以BC为直径的半圆O交于AB于D,DE⊥AC于E.求证:DE是半圆O的切线.
如图,△ABC中,CA=CB,以BC为直径的半圆O交于AB于D,DE⊥AC于E.求证:DE是半圆O的切线.