题目内容
1.若m、n满足|m+1|+$\sqrt{n-2}$=0,则mn=1.分析 根据非负数的性质可求出m、n的值,进而可求出mn的值.
解答 解:∵|m+1|+$\sqrt{n-2}$=0,
∴m+1=0,n-2=0,
∴m=-1,n=2,
∴mn=1,
故答案为:1.
点评 此题主要考查了非负数的性质,初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列方程是一元二次方程的是( )
| A. | x2+3y-5=0 | B. | $\frac{1}{x}$-2x2+1=0 | ||
| C. | ax2+bx+c=0(其中a、b、c为常数) | D. | $\sqrt{3}$x2+4x-5=0 |
13.2008年5月12日,四川汶川发生8.3级大地震,据统计这次地震直接经济损失大约600 000 000 000元,这个数据用科学记数法表示为( )
| A. | 0.6×1012元 | B. | 6×1012元 | C. | 6×1011元 | D. | 60×1010元 |
10.an=3,am=2,a2n-3m=( )
| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{9}{8}$ | D. | $\frac{11}{8}$ |
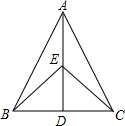 已知:如图,AB=AC,AD⊥BC于D,点E在AD上,图中共有3对全等三角形.
已知:如图,AB=AC,AD⊥BC于D,点E在AD上,图中共有3对全等三角形.