Question

4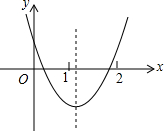．已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，则下列结论：（1）4a+2b+c＞0；（2）$\frac{ab}{c}$＜0；（3）一次函数y=x+bc一定不过第二象限；（4）$\frac{4ac-{b}^{2}}{4a}$＜a+b+c，其中正确的是①②③④．

Answer 1

分析 （1）由函数图象可知x=2对应的抛物线图象上的点在x轴上方，故把x=2代入抛物线解析式得到的函数值大于0，本选项正确；
（2）由a的符号及对称轴在y轴的右侧判断出b的符号，再由抛物线与y轴的交点在y轴正半轴判断出c的符号，进而得出$\frac{ab}{c}$符号，本选项正确．
（3）根据b、c的符合，得出bc的符合，根据一次函数的图象与性质可得出y=x+bc不经过第二象限，本选项正确．
（4）根据抛物线的最低点，即可得出$\frac{4ac-{b}^{2}}{4a}$＜a+b+c，本选项正确．

解答 解：（1）由函数图象可知x=2对应的抛物线图象上的点在x轴上方，故把x=2代入抛物线解析式得到4a2+b+c＞0，本选项正确；
（2）开口向上a＞0，-$\frac{b}{2a}$＞0，∴b＜0，交于y轴正半轴c＞0，
∴$\frac{ab}{c}$＜0，本选项正确；
（3）由y=x+bc中，k=1，bc为常数项，
∵a＞0，-$\frac{b}{2a}$＞0，∴b＜0，交于y轴正半轴c＞0，
∴bc＜0，则一次函数y=x+bc经过第一、三、四象限，不经过第二象限，本选项正确；
（4）由图象可知：抛物线有最低点，∴$\frac{4ac-{b}^{2}}{4a}$＜a+b+c，本选项正确；
综上，正确的个数有①②③④4个．
故答案为①②③④．

点评 此题考查了二次函数的图象与系数的关系，图象的增减性以及二次函数与方程之间的关系，利用了数形结合的思想，此类题涉及的知识面比较广，能正确观察图象是解本题的关键．