题目内容
求直线y=2x+6,y=-2x-8与y轴所围成图形的面积.
考点:两条直线相交或平行问题
专题:
分析:求出两直线与y轴的交点坐标,再联立两直线解析式求出交点坐标,然后根据三角形的面积公式列式计算即可得解.
解答:解:令x=0,则y=2x+6=6,所以,直线y=2x+6与y轴的交点坐标为(0,6),
令x=0,则y=-2x-8=-8,所以,直线y=-2x-8与y轴的交点坐标为(0,-8),
联立
,
解得
,
所以,两直线的交点坐标是(-
,-1),
两直线与y轴所围成的图形的面积S=
(6+8)×
=
.
令x=0,则y=-2x-8=-8,所以,直线y=-2x-8与y轴的交点坐标为(0,-8),
联立
|
解得
|
所以,两直线的交点坐标是(-
| 7 |
| 2 |
两直线与y轴所围成的图形的面积S=
| 1 |
| 2 |
| 7 |
| 2 |
| 49 |
| 2 |
点评:本题考查了两直线相交的问题,联立两直线解析式,解方程组求交点坐标是常用的方法,一定要熟练掌握并灵活运用.

练习册系列答案
相关题目
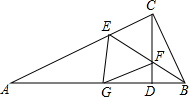 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,BE平分∠ABC交AC于E,交CD于F,FG∥CA于G,求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,BE平分∠ABC交AC于E,交CD于F,FG∥CA于G,求证:四边形CEGF是菱形. 如图是一块地,已知AD=8cm,CD=6cm,∠D=90°,AB=26cm,BC=24cm,求这块地的面积.
如图是一块地,已知AD=8cm,CD=6cm,∠D=90°,AB=26cm,BC=24cm,求这块地的面积.