题目内容
若关于x的一元二次方程x2+(2m-1)x+m2=0有两个实数根x1和x2.
(1)求实数m的范围;
(2)当|x1|-|x2|=0时,求m的值.
(1)求实数m的范围;
(2)当|x1|-|x2|=0时,求m的值.
考点:根的判别式,根与系数的关系
专题:
分析:(1)根据方程有实数根,可得△≥0,解不等式,可得答案;
(2)由|x1|-|x2|=0,可得x1+x2=0或x1-x2=0,根据根与系数的关系,可得答案.
(2)由|x1|-|x2|=0,可得x1+x2=0或x1-x2=0,根据根与系数的关系,可得答案.
解答:解:(1)∵关于x的一元二次方程x2+(2m-1)x+m2=0有两个实数根x1和x2,
∴△=b2-4ac=(2m-1)2-4×1×m2=-4m+1≥0,
解得m≤
;
(2)由根与系数的关系,可得根x1+x2=-(2m-1),
由|x1|-|x2|=0,得x1+x2=0或x1-x2=0.
当x1+x2=0时,即x1+x2=-(2m-1)=0,解得m=
(不符合题意的要舍去);
当x1-x2=0时,△=b2-4ac=(2m-1)2-4×1×m2=-4m+1=0,
解得m=
.
∴△=b2-4ac=(2m-1)2-4×1×m2=-4m+1≥0,
解得m≤
| 1 |
| 4 |
(2)由根与系数的关系,可得根x1+x2=-(2m-1),
由|x1|-|x2|=0,得x1+x2=0或x1-x2=0.
当x1+x2=0时,即x1+x2=-(2m-1)=0,解得m=
| 1 |
| 2 |
当x1-x2=0时,△=b2-4ac=(2m-1)2-4×1×m2=-4m+1=0,
解得m=
| 1 |
| 4 |
点评:本题考查了根的判别式,利用了根的判别式,根与系数的关系.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,以OA为直径的⊙C与⊙O的弦AD相交于点E,图中有哪些相等的线段?
如图,AB是⊙O的直径,以OA为直径的⊙C与⊙O的弦AD相交于点E,图中有哪些相等的线段?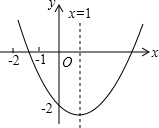 已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,有下列结论: 如图,直角梯形OABC,CB∥OA,OC=4
如图,直角梯形OABC,CB∥OA,OC=4 如图,A是半径为1的⊙O的外一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥AO,连结AC,则图中的阴影部分的面积等于
如图,A是半径为1的⊙O的外一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥AO,连结AC,则图中的阴影部分的面积等于