题目内容
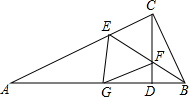 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,BE平分∠ABC交AC于E,交CD于F,FG∥CA于G,求证:四边形CEGF是菱形.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,BE平分∠ABC交AC于E,交CD于F,FG∥CA于G,求证:四边形CEGF是菱形.考点:菱形的判定
专题:证明题
分析:利用角平分线的性质首先得出DF=FN,进而得出FC=GF,即可利用互余关系得出EC=FG,进而求出四边形CEGF是平行四边形进而求出它是菱形.
解答: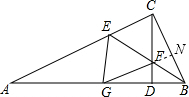 证明:延长GF交BC于点N,
证明:延长GF交BC于点N,
∵GF∥AC,
∴GN∥AC,
∴∠ACB=∠GNB=90°,
∵BE平分∠ABC交AC于E,∠FDB=∠FNB=90°,
∴FD=FN,
在Rt△BFN和Rt△BFD中
,
∴Rt△BFN≌Rt△BFD(HL),
∴BD=BN,
在△CDB和△GNB中
,
∴△CDB≌△GNB(ASA),
∴DC=GN,
∴CF=FG,
∵∠CEB+∠EBC=90°,
∠EBD+∠BFD=90°,∠CBE=∠DBF,
∴∠CEB=∠BFD,
又∵∠BFD=∠EFC,
∴∠CEB=∠CFE,
∴CE=CF,
∴CE=GF,
又∵FG∥AC,
∴四边形CEGF是平行四边形,
又∵FC=FG,
∴四边形CEGF是菱形.
 证明:延长GF交BC于点N,
证明:延长GF交BC于点N,∵GF∥AC,
∴GN∥AC,
∴∠ACB=∠GNB=90°,
∵BE平分∠ABC交AC于E,∠FDB=∠FNB=90°,
∴FD=FN,
在Rt△BFN和Rt△BFD中
|
∴Rt△BFN≌Rt△BFD(HL),
∴BD=BN,
在△CDB和△GNB中
|
∴△CDB≌△GNB(ASA),
∴DC=GN,
∴CF=FG,
∵∠CEB+∠EBC=90°,
∠EBD+∠BFD=90°,∠CBE=∠DBF,
∴∠CEB=∠BFD,
又∵∠BFD=∠EFC,
∴∠CEB=∠CFE,
∴CE=CF,
∴CE=GF,
又∵FG∥AC,
∴四边形CEGF是平行四边形,
又∵FC=FG,
∴四边形CEGF是菱形.
点评:此题主要考查了菱形的判定以及全等三角形的判定与性质和角平分线的性质,得出FG=FC是解题关键.

练习册系列答案
相关题目
 如图,已知PA是⊙O的切线,P为切点,PA=5
如图,已知PA是⊙O的切线,P为切点,PA=5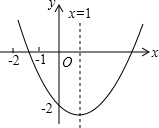 已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(x≠0)的图象如图所示,有下列结论: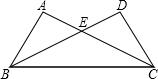 如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.