题目内容
 如图是一块地,已知AD=8cm,CD=6cm,∠D=90°,AB=26cm,BC=24cm,求这块地的面积.
如图是一块地,已知AD=8cm,CD=6cm,∠D=90°,AB=26cm,BC=24cm,求这块地的面积.考点:勾股定理,勾股定理的逆定理
专题:
分析:根据勾股定理可求出AC的长,根据勾股定理的逆定理可求出∠ACB=90°,可求出△ACB的面积,减去△ACD的面积,可求出四边形ABCD的面积.
解答: 解:如图,连接AC.
解:如图,连接AC.
∵CD=6cm,AD=8cm,∠ADC=90°,
∴AC=
=10(cm).
∵AB=26cm,BC=24cm,102+242=262.即AC2+BC2=AB2,
∴△ABC为直角三角形,∠ACB=90°.
∴四边形ABCD的面积=S△ABC-S△ACD=
×10×24-
×6×8=96(cm2).
 解:如图,连接AC.
解:如图,连接AC.∵CD=6cm,AD=8cm,∠ADC=90°,
∴AC=
| 62+82 |
∵AB=26cm,BC=24cm,102+242=262.即AC2+BC2=AB2,
∴△ABC为直角三角形,∠ACB=90°.
∴四边形ABCD的面积=S△ABC-S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了勾股定理和勾股定理的逆定理,关键判断出直角三角形从而可求出面积.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,以OA为直径的⊙C与⊙O的弦AD相交于点E,图中有哪些相等的线段?
如图,AB是⊙O的直径,以OA为直径的⊙C与⊙O的弦AD相交于点E,图中有哪些相等的线段? 如图,A是半径为1的⊙O的外一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥AO,连结AC,则图中的阴影部分的面积等于
如图,A是半径为1的⊙O的外一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥AO,连结AC,则图中的阴影部分的面积等于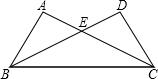 如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC. 如图,已知AB是一条直线,OC是∠AOD的平分线,OE是∠BOD的平分线.若∠EOD:∠COD=2:3,求∠COD及∠BOC的度数.
如图,已知AB是一条直线,OC是∠AOD的平分线,OE是∠BOD的平分线.若∠EOD:∠COD=2:3,求∠COD及∠BOC的度数.