题目内容
16.在等边△ABC中,点D为AC上一点,连接BD,直线l与AB,BD,BC分别相交于点E,P,F,且∠BPF=60°.(1)如图(1),写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)若直线l向右平移到图(2),图(3)的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不需证明),若不成立,请说明理由;
(3)探究:如图(1),当BD满足什么条件时(其它条件不变),EF=$\sqrt{3}$BF?请写出探究结果,并说明理由.

分析 (1)先判断出∠BPF=∠EBF=60°,再结合公共角即可得出结论;
(2)同(2)的方法即可得出结论;
(3)先判断出∠BEF=30°,再利用锐角三角函数即可得出结论.
解答 解:(1)△BPF∽△EBF,△BPF∽△BCD,
理由:∵等边△ABC中,∴∠EPF=60°,
∴∠BPF=∠EBF=60°,∠BFP=∠BFE,
∴△BPF∽△EBF,
同理:△BPF∽△BCD
(2)成立,△BPF∽△EBF,△BPF∽△BCD,
理由:∵等边△ABC中,∴∠EPF=60°,
∴∠BPF=∠EBF=60°,∠BFP=∠BFE,
∴△BPF∽△EBF,
同理:△BPF∽△BCD
(3)当BD平分∠ABC时,EF=$\sqrt{3}$BF,
理由:∵BD平分∠ABC,
∴∠ABP=∠PBF=30°,
∵∠BPF=60°,∠BFP=90°,
∴∠BEF=60°-30°=30°,
在Rt△BEF中,∠EBF=60°,
∴tan60°=$\frac{EF}{BF}$,
即:EF=$\sqrt{3}$BF.
点评 此题是相似形综合题,主要考查了等边三角形的性质,相似三角形的判定,锐角三角函数的意义,解本题的关键是求出∠EBF=60°,是一道比较简单的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )
如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )
 如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )
如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )| A. | 4π | B. | 8π | C. | 10π | D. | 15π |
8.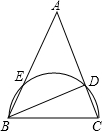 如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )
如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )
 如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )
如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )| A. | 40° | B. | 70° | C. | 50° | D. | 20° |
5.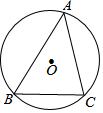 如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )
 如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )| A. | $\frac{3}{4}$π | B. | $\frac{3}{2}$ π | C. | $\frac{45}{2}$ π | D. | $\frac{9}{4}$ π |
6.下列计算正确的是( )
| A. | -5+2=-7 | B. | 6÷(-2)=-3 | C. | -7-2=9 | D. | -22=4 |
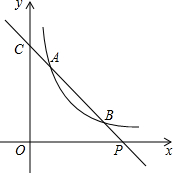 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.已知A,B两点的坐标分别为(1,3),(3,y2).
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.已知A,B两点的坐标分别为(1,3),(3,y2).