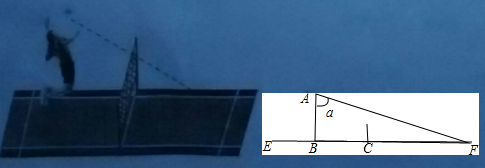
题目内容
16．
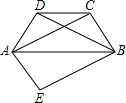如图，在四边形ABCD中，AB∥CD，AD=BC，AC，BD是对角线且AC=BD．将△ABD沿AB对折到△ABE的位置，求证：四边形AEBC是平行四边形．
分析 根据折叠性质得出△ABD≌△ABE，根据全等三角形的性质得出BD=BE，AD=AE，求出AE=BC，BE=AC，根据平行四边形的判定得出即可．
解答 证明：∵将△ABD沿AB对折到△ABE的位置，
∴△ABD≌△ABE，
∴BD=BE，AD=AE，
∵AD=BC，AC=BD，
∴AE=BC，BE=AC，
∴四边形AEBC是平行四边形．
点评 本题考查了全等三角形的性质，折叠的性质，平行四边形的判定的应用，能求出AE=BC，BE=AC是解此题的关键，注意：有两组对边分别相等的四边形是平行四边形．
练习册系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
6．
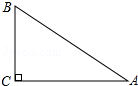如图，在Rt△ABC中，∠C=90°，BC=6，AC=8，那么sinA的值等于（ ）
如图，在Rt△ABC中，∠C=90°，BC=6，AC=8，那么sinA的值等于（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
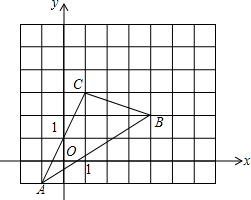如图，△ABC在直角坐标系中，