题目内容
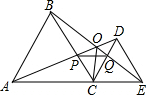 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.则四个结论:①AD=BE;②∠OED=∠EAD;③∠AOB=60°; ④DE=DP中错误的是( )
| A、① | B、② | C、③ | D、④ |
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:根据等边三角形的性质就可以得出△ACD≌△BCE,∠ACB=∠CED=60°,就有BC∥DE,∠OED=∠CBE,由∠CBE=∠CAD而得出结论,∠DPC=∠PCA+∠PAC=60°+∠CAP>∠DCP=60°而得出DE≠DP从而得出结论.
解答:解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,EC=DC=DE,∠ACB=∠DCE=∠DEC=60°,
∴BC∥DE,∠ACB+BCD=∠DCE+∠BCD,
∴∠OED=∠CBE,∠ACD=∠BCE.
在△ACD和△BCE在
,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE.AD=BE,故①正确;
∴∠OED=∠EAD.故②正确.
∵∠AOB=∠EAD+∠AEO,
∴∠AOB=∠CBE+∠AEO.
∵∠CBE+∠AEO=∠ACB=60°,
∴∠AOB=60°.故③正确
∵∠ACB+∠DCE+∠BCD=180°,
∴∠BCD=60°.
∵∠DPC=∠PCA+∠PAC=60°+∠CAP>∠DCP=60°,
∴DE≠DP.故④错误.
故选D.
∴AC=BC,EC=DC=DE,∠ACB=∠DCE=∠DEC=60°,
∴BC∥DE,∠ACB+BCD=∠DCE+∠BCD,

∴∠OED=∠CBE,∠ACD=∠BCE.
在△ACD和△BCE在
|
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE.AD=BE,故①正确;
∴∠OED=∠EAD.故②正确.
∵∠AOB=∠EAD+∠AEO,
∴∠AOB=∠CBE+∠AEO.
∵∠CBE+∠AEO=∠ACB=60°,
∴∠AOB=60°.故③正确
∵∠ACB+∠DCE+∠BCD=180°,
∴∠BCD=60°.
∵∠DPC=∠PCA+∠PAC=60°+∠CAP>∠DCP=60°,
∴DE≠DP.故④错误.
故选D.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,平行线的判定及性质的运用,三角形的外角与内角的关系的运用,解答时证明三角形全等是关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
若x,y为实数,且|x+1|+
=0,则(
)2013的值是( )
| y-1 |
| x |
| y |
| A、0 | B、1 | C、-1 | D、-2013 |
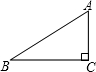 如图,在△ABC中,∠C=90°,AC=3,BC=4,则sinB的值是( )
如图,在△ABC中,∠C=90°,AC=3,BC=4,则sinB的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
在直角坐标系中,点A(a,5),B(3,b)关于x轴对称,则a+b=( )
| A、-8 | B、2 | C、-2 | D、8 |
下列命题中,正确的是( )
| A、相似三角形是全等的三角形 |
| B、一个角为30°的两个等腰三角形相似 |
| C、全等三角形都是相似三角形 |
| D、所有等腰直角三角形不一定相似 |
若A=4x2-3x-2,B=4x2-3x-4,则A,B的大小关系是( )
| A、A<B | B、A=B |
| C、A>B | D、无法确定 |