题目内容
下面三道解方程,解法正确的个数是( )
(1)解方程3x2=4.解:3x=±2,∴x=±
.
(2)解方程x2=2x.解:方程的两边同除以x,得x=2.
(3)解方程(x-2)(x-3)=1.解:由x-2=1得x=3,由x-3=1得x=4.
(1)解方程3x2=4.解:3x=±2,∴x=±
| 2 |
| 3 |
(2)解方程x2=2x.解:方程的两边同除以x,得x=2.
(3)解方程(x-2)(x-3)=1.解:由x-2=1得x=3,由x-3=1得x=4.
| A、0 | B、1 | C、2 | D、3 |
考点:解一元二次方程-因式分解法,解一元二次方程-直接开平方法,解一元二次方程-公式法
专题:计算题
分析:求出各方程的解,即可做出判断.
解答:解:(1)解方程3x2=4.
解:
x=±2,
∴x=±
,错误;
(2)解方程x2=2x.
解:移项得:x2-2x=0,分解因式得:x(x-2)=0,
解得:x1=0,x2=2;错误;
(3)解方程(x-2)(x-3)=1.
解:方程整理得:x2-5x+5=0,
这里a=1,b=-5,c=5,
∵△=25-20=5,
∴x=
,错误,
则正确个数为0.
故选A.
解:
| 3 |
∴x=±
2
| ||
| 3 |
(2)解方程x2=2x.
解:移项得:x2-2x=0,分解因式得:x(x-2)=0,
解得:x1=0,x2=2;错误;
(3)解方程(x-2)(x-3)=1.
解:方程整理得:x2-5x+5=0,
这里a=1,b=-5,c=5,
∵△=25-20=5,
∴x=
5±
| ||
| 2 |
则正确个数为0.
故选A.
点评:此题考查了解一元二次方程-因式分解法,以及公式法,熟练掌握各种解法是解本题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
下列条件中,能判断两个三角形全等的是( )
| A、一个钝角相等的两个等腰三角形 |
| B、两个含60°的直角三角形 |
| C、边长为3和6的两个等腰三角形 |
| D、有一条边对应相等的两个直角三角形 |
大于-2.5而小于
的整数共有( )
| 5 |
| A、6个 | B、5个 | C、4个 | D、3个 |
方程x2+x=0的解是( )
| A、x=±1 |
| B、x=0 |
| C、x1=0,x2=-1 |
| D、x=1 |
不能进行密铺的图形是( )
| A、正三边形 | B、正四边形 |
| C、正五边形 | D、正六边形 |
下列命题是真命题的是( )
| A、两边及一个角对应相等的两三角形全等 |
| B、两角及一边对应相等的两三角形全等 |
| C、三个角对应相等的两三角形全等 |
| D、面积相等的两三角形全等 |
若代数式3x4y与-xmy是同类项,则常数m的值为( )
| A、1 | B、2 | C、3 | D、4 |
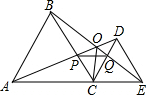 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ. 请你在图中画出在点O的:
请你在图中画出在点O的: