题目内容
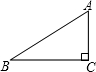如图，在△ABC中，∠C=90°，AC=3，BC=4，则sinB的值是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：锐角三角函数的定义,勾股定理
专题：
分析：首先利用勾股定理计算出AB，再根据正弦定义进行计算．
解答：解：∵∠C=90°，AC=3，BC=4，
∴AB=
=5，
∴sinB=
=
，
故选：C．
∴AB=
| 32+42 |
∴sinB=
| AC |
| AB |
| 3 |
| 5 |
故选：C．
点评：此题主要考查了勾股定理，以及锐角三角函数定义，关键是掌握正弦：锐角A的对边a与斜边c的比叫做∠A的正弦．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
已知⊙O1和⊙O2的半径分别为2和5，O1O2=6，则⊙O1和⊙O2的位置关系是（ ）
| A、外切 | B、内切 | C、相交 | D、外离 |
以下各组数分别是三条线段的长度，其中可以构成三角形的是（ ）
| A、1，3，4 |
| B、1，2，3 |
| C、6，6，10 |
| D、1，4，6 |
大于-2.5而小于
的整数共有（ ）
| 5 |
| A、6个 | B、5个 | C、4个 | D、3个 |
在⊙O中，弦AB和弦CD，如果AB=2CD，下列正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、无法确定 |
方程x2+x=0的解是（ ）
| A、x=±1 |
| B、x=0 |
| C、x1=0，x2=-1 |
| D、x=1 |
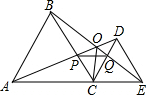如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边三角形ABC和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．
如图，点A在x轴正半轴上OB=4，∠AOB=30°，BA⊥x轴于A．