题目内容
在直角坐标系中,点A(a,5),B(3,b)关于x轴对称,则a+b=( )
| A、-8 | B、2 | C、-2 | D、8 |
考点:关于x轴、y轴对称的点的坐标
专题:
分析:根据关于x轴对称的点,横坐标相同,纵坐标互为相反数,解答即可.
解答:解:∵点A(a,5)和(3,b)关于x轴对称,
∴a=3,b=-5,
∴a+b=3-5=-2.
故选:C.
∴a=3,b=-5,
∴a+b=3-5=-2.
故选:C.
点评:本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.
(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;
(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;
(3)关于原点对称的点,横坐标与纵坐标都互为相反数.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
以下各组数分别是三条线段的长度,其中可以构成三角形的是( )
| A、1,3,4 |
| B、1,2,3 |
| C、6,6,10 |
| D、1,4,6 |
在⊙O中,弦AB和弦CD,如果AB=2CD,下列正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、无法确定 |
方程x2+x=0的解是( )
| A、x=±1 |
| B、x=0 |
| C、x1=0,x2=-1 |
| D、x=1 |
有4条线段,长分别是:2,3,4,5,从中任取3条,可以组成三角形的情况有( )
| A、0种 | B、1种 | C、2种 | D、3种 |
在△ABC中,不能判断△ABC为直角三角形的条件是( )
| A、∠C=∠A-∠B | ||||
| B、∠A:∠B:∠C=5:2:3 | ||||
C、a=
| ||||
| D、a:b:c=2:2:4 |

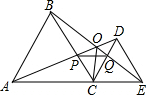 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.