题目内容
下列命题中，正确的是（ ）
| A、相似三角形是全等的三角形 |
| B、一个角为30°的两个等腰三角形相似 |
| C、全等三角形都是相似三角形 |
| D、所有等腰直角三角形不一定相似 |
考点：相似三角形的判定,命题与定理
专题：
分析：根据相似三角形的性质与判定，结合选项进行判断．
解答：解：A、相似三角形不一定是全等的三角形，全等只是相似的一种特殊情况，故本选项错误；
B、不确定30°的角是顶角还是底角，故不能判断相似，故本选项错误；
C、全等三角形都是相似三角形，说法正确，故本选项正确；
D、所有等腰直角三角形一定相似，故本选项错误．
故选C．
B、不确定30°的角是顶角还是底角，故不能判断相似，故本选项错误；
C、全等三角形都是相似三角形，说法正确，故本选项正确；
D、所有等腰直角三角形一定相似，故本选项错误．
故选C．
点评：本题考查了相似三角形的判定，注意所有的全等图形都相似，所有的等腰直角三角形都相似．
练习册系列答案
相关题目
在⊙O中，弦AB和弦CD，如果AB=2CD，下列正确的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、无法确定 |
有4条线段，长分别是：2，3，4，5，从中任取3条，可以组成三角形的情况有（ ）
| A、0种 | B、1种 | C、2种 | D、3种 |
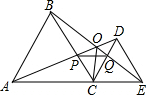如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边三角形ABC和等边三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ．（-2）100+（-2）101的结果是（ ）
| A、2100 |
| B、-2100 |
| C、-2 |
| D、2 |
在△ABC中，不能判断△ABC为直角三角形的条件是（ ）
| A、∠C=∠A-∠B | ||||
| B、∠A：∠B：∠C=5：2：3 | ||||
C、a=
| ||||
| D、a：b：c=2：2：4 |
如图，已知数轴上有A、B、C三个点，它们表示的数分别是-24，-10，10．