题目内容
1.已知:x=2+$\sqrt{3}$,y=2-$\sqrt{3}$,求x2+y2-3xy-5x+5y的值.分析 首先由x=2+$\sqrt{3}$,y=2-$\sqrt{3}$,求得x-y和xy,进一步分组分解代数式,再整体代入求得答案即可.
解答 解:∵x=2+$\sqrt{3}$,y=2-$\sqrt{3}$,
∴x-y=2$\sqrt{3}$,xy=1,
∴x2+y2-3xy-5x+5y
=(x-y)2-xy-5(x-y)
=(2$\sqrt{3}$)2-1-5×2$\sqrt{3}$
=11-10$\sqrt{3}$.
点评 此题考查二次根式的混合运算,渗透整体代入的思想.

练习册系列答案
相关题目
13.下列命题是真命题的是( )
| A. | 内错角相等 | |
| B. | 如果a2=b2,那么a3=b3 | |
| C. | 三角形的一个外角大于任何一个内角 | |
| D. | 平行于同一直线的两条直线平行 |
11.已知代数式$\frac{1}{2}$xa-1y3与-3xby2a-b是同类项,那么a,b的值分别是( )
| A. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ |
 如图,在正方形ABCD中,CE⊥DF,求证:CE=DF.
如图,在正方形ABCD中,CE⊥DF,求证:CE=DF.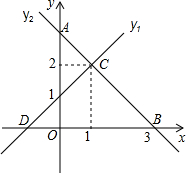 如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有①②③(直接写序号)
如图,直线y1与y2相交于点C(1,2),y1与x轴交于点D,与y轴交于点(0,1);y2与x轴交于点B(3,0),与y轴交于点A.下列说法正确的有①②③(直接写序号)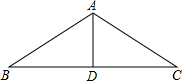 如图,已知房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数.
如图,已知房屋的顶角∠BAC=100°,过屋顶A的立柱AD⊥BC,屋椽AB=AC,求顶架上∠B、∠C、∠BAD、∠CAD的度数.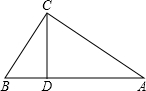 已知,如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D.
已知,如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D.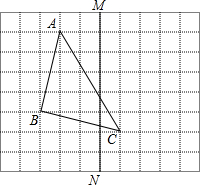 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上.