题目内容
观察各式:12+1=1×2;22+2=2×3;32+3=3×4.
(1)请你按规律写出第10个等式;
(2)将你猜想到的规律用自然数n(n≥1)表示出来.
(1)请你按规律写出第10个等式;
(2)将你猜想到的规律用自然数n(n≥1)表示出来.
考点:规律型:数字的变化类
专题:规律型
分析:(1)观察不难发现,一个数的平方加上它本身等于这个数乘比它大1的数;
(2)根据(1)中观察出的规律写出即可.
(2)根据(1)中观察出的规律写出即可.
解答:解:(1)∵12+1=1×2;22+2=2×3;32+3=3×4,
∴第10个等式为102+10=10×11;
(2)规律为n2+n=n(n+1).
∴第10个等式为102+10=10×11;
(2)规律为n2+n=n(n+1).
点评:本题是对数字变化规律的考查,比较简单,注意等式右边的两个数与左边的数的关系是解题的关键.

练习册系列答案
相关题目
解方程-3x+5=2x-1时,移项正确的是( )
| A、3x-2x=-1+5 |
| B、-3x-2x=5-1 |
| C、3x-2x=-1-5 |
| D、-3x-2x=-1-5 |
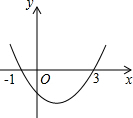 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b+2a=0②abc<0③a-2b+4c<0④8a+c>0,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b+2a=0②abc<0③a-2b+4c<0④8a+c>0,其中正确的有( )| A、3个 | B、2个 | C、1个 | D、0个 |
若x2+kx+16能通过因式分解写成(a+b)2的形式,则k的值是( )
| A、8 | B、-8 | C、±8 | D、±4 |
 如图,已知斜坡MN的坡脚N处有一颗大树PN,太阳光线以45°的俯角将树顶P的影子落在斜坡MN上的点Q处.如果大树PN在斜坡MN上的影子NQ长为6.5米,大树PN高为8.5米,求斜坡MN的坡度.
如图,已知斜坡MN的坡脚N处有一颗大树PN,太阳光线以45°的俯角将树顶P的影子落在斜坡MN上的点Q处.如果大树PN在斜坡MN上的影子NQ长为6.5米,大树PN高为8.5米,求斜坡MN的坡度.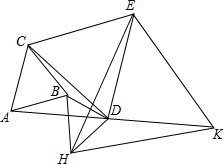 如图,位于同一平面内的正△ABC、正△CDE和正△EHK(顶点依逆时针方向排列),两两地有公共点C和E,且D是AK的中点,求证:△BHD也是正三角形.
如图,位于同一平面内的正△ABC、正△CDE和正△EHK(顶点依逆时针方向排列),两两地有公共点C和E,且D是AK的中点,求证:△BHD也是正三角形.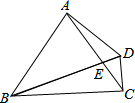 如图,△ABC是等边三角形,BD=AB,BD与AC交于点E,当点E在AC上运动时,∠ADC的大小是否发生变化?如果变化,请说明变化的范围,如果不变,请说明理由.
如图,△ABC是等边三角形,BD=AB,BD与AC交于点E,当点E在AC上运动时,∠ADC的大小是否发生变化?如果变化,请说明变化的范围,如果不变,请说明理由.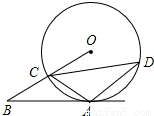 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,且C为OB的中点,过C点作弦CD,若∠ACD=45°,AD=2.求AC的长.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,且C为OB的中点,过C点作弦CD,若∠ACD=45°,AD=2.求AC的长.