题目内容
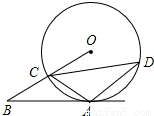 如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,且C为OB的中点,过C点作弦CD,若∠ACD=45°,AD=2.求AC的长.
如图,AB是⊙O的切线,A为切点,OB交⊙O于点C,且C为OB的中点,过C点作弦CD,若∠ACD=45°,AD=2.求AC的长.考点:切线的性质
专题:计算题
分析:连结OA,OD,如图,根据切线的性质得∠OAB=90°,由于C为OB的中点,根据直角三角形斜边上的中线性质得AC=OC=CA,再利用圆周角定理得∠AOD=2∠ACD=90°,则△ODA为等腰直角三角形,所以OD=
AD=
,则AC=
.
| ||
| 2 |
| 2 |
| 2 |
解答:解:连结OA,OD,如图,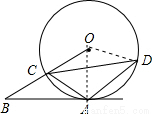
∵AB是⊙O的切线,
∴OA⊥AB,
∴∠OAB=90°,
∵C为OB的中点,
∴AC=OC=CA,
∵∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∴△ODA为等腰直角三角形,
∴OD=
AD=
×2=
,
∴AC=
.

∵AB是⊙O的切线,
∴OA⊥AB,
∴∠OAB=90°,
∵C为OB的中点,
∴AC=OC=CA,
∵∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∴△ODA为等腰直角三角形,
∴OD=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴AC=
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
 如图,量角器上的C、D两点所表示的读数分别是80°、50°,则∠DBC的度数为( )
如图,量角器上的C、D两点所表示的读数分别是80°、50°,则∠DBC的度数为( )| A、25° | B、15° |
| C、30° | D、50° |
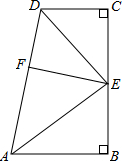 如图,∠B=∠C=90°,E是BC的中点,EF⊥AD于点F,DE平分∠ADC,∠CED=35°,则∠EAB=
如图,∠B=∠C=90°,E是BC的中点,EF⊥AD于点F,DE平分∠ADC,∠CED=35°,则∠EAB= 已知:如图,AB=DC,AE=BF,CE=DF.
已知:如图,AB=DC,AE=BF,CE=DF. 如图,已知C为线段AE上的一个动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,连接AD、BE.求证:AD=BE.
如图,已知C为线段AE上的一个动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,连接AD、BE.求证:AD=BE.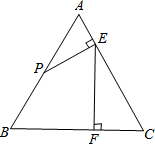 已知:如图所示,等边三角形ABC的边长为2cm,点P从A点开始,沿AB方向作匀速运动,到B点时运动停止,运动速度为2cm/s,过P点作PE⊥AC于E点,再过E点作EF⊥BC于F点.
已知:如图所示,等边三角形ABC的边长为2cm,点P从A点开始,沿AB方向作匀速运动,到B点时运动停止,运动速度为2cm/s,过P点作PE⊥AC于E点,再过E点作EF⊥BC于F点.